如图所示, 质量为M的平板车P高h,质量为m的小物块Q的大小不计,位于平板车的左端,系统原来静止在光滑水平面地面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系
质量为M的平板车P高h,质量为m的小物块Q的大小不计,位于平板车的左端,系统原来静止在光滑水平面地面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系 一质量也为m的小球(大小不计).今将小球拉至悬线与竖直位置成60°角,由静止释放,小球到达最低点时与Q的碰撞时间极短,且无能量损失,已
一质量也为m的小球(大小不计).今将小球拉至悬线与竖直位置成60°角,由静止释放,小球到达最低点时与Q的碰撞时间极短,且无能量损失,已 知Q离开平板车时速度大小是平板车速度的两倍,Q与P之间的动摩擦因数为μ,M:m=4:1,重力加速度为g.求:
知Q离开平板车时速度大小是平板车速度的两倍,Q与P之间的动摩擦因数为μ,M:m=4:1,重力加速度为g.求: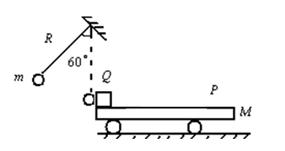
(1)小物块Q离开平板车时速度为多大?
(2)平板车P的长度为多少?
(3)小物块Q落地时距小球的水平距离为多少?
(1)如图1所示, 为一固定在竖直平面内的光滑轨道, 段水平, 段与 段平滑连接。质量为 的小球从高位 处由静止开始沿轨道下滑,与静止在轨道 段上质量为 的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球 的速度大小 。

(2)碰撞过程中的能量传递规律在屋里学中有着广泛的应用。为了探究这一规律,我们才用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的恶简化力学模型。如图2所示,在固定光滑水平轨道上,质量分别为
的若干个球沿直线静止相间排列,给第1个球初能
,从而引起各球的依次碰撞。定义其中第
个球经过依次碰撞后获得的动能
与
之比为第1个球对第 个球的动能传递系数
。
个球的动能传递系数
。
a.求
;
b.若
为确定的已知量。求
为何值时,
值最大。

某同学通过查找资料自己动手制作了一个电池。该同学想测量一下这个电池的电动势E 和内电阻 ,但是从实验室只借到一个开关、一个电阻箱(最大阻值为9.999
,但是从实验室只借到一个开关、一个电阻箱(最大阻值为9.999 ,科当标准电阻用)一只电流表(量程
,科当标准电阻用)一只电流表(量程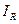 =0.6A,内阻
=0.6A,内阻 )和若干导线。
)和若干导线。
①请根据测定电动势E内电阻 的要求,设计图4中器件的连接方式,画线把它们连接起来。
的要求,设计图4中器件的连接方式,画线把它们连接起来。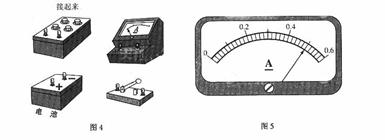
②接通开关,逐次改变电阻箱的阻值 ,
,
读处与 对应的电流表的示数I,并作记录
对应的电流表的示数I,并作记录
当电阻箱的阻值 时,
时,
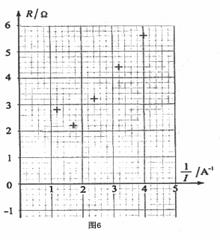
其对应的电流表的示数如图5所示。处理实验数据时
首先计算出每个电流值I 的倒数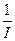 ;再制作R-
;再制作R-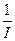 坐标图,如图
坐标图,如图
6所示,图中已标注出了(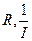 )的几个与测量对应的坐标点,请你将与图5实验数据对应的坐标点也标注在图6中上。
)的几个与测量对应的坐标点,请你将与图5实验数据对应的坐标点也标注在图6中上。
③在图6上把描绘出的坐标点练成图线。
④根据图6描绘出的图线可得出这个
电池的电动势E=V,内电阻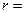

一块玻璃砖有两个相互平行的表面,其中一个表面是镀银的(光线不能通过此表面).现要测定此玻璃的折射率,给定的器材还有:白纸、铅笔、大头针4枚(P1、P2、P3、P4)、带有刻度的直角三角板、量角器.实验时,先将玻璃砖放到白纸上,使上述两个相互平行的表面与纸面垂直.在纸面上画出直线aa′和 bb′,aa′表示镀银的玻璃表面,bb′表示另一表面,如图6所示.然后,在白纸上竖直插上两枚大头针P1、P2(位置如图).用P1、P2的连线表示入射光线.
为了测量折射率,应如何正确使用大头针P3、P4?
试在题图中标出P3、P4的位置.然后,移去玻璃砖与大头针.试在题图中通过作图的方法标出光线从空气到玻璃中的入射角
 1与折射角θ2.简要写出作图步骤.
1与折射角θ2.简要写出作图步骤.写出用θ1、θ2表示的折射率公式为n=.

在场强为
的水平匀强磁场中,一质量为
、带正电
的小球在
静止释放,小球的运动曲线如图所示.已知此曲线在最低点的曲率半径为该点到
轴距离的2倍,重力加速度为
.求:
(1)小球运动到任意位置
的速率
(2)小球在运动过程中第一次下降的最大距离 .
(3)当在上述磁场中加一竖直向上场强为 的匀强电场时,小球从 静止释放后获得的最大速率 .
某电流表的内阻在0.1Ω~0.2Ω之间,现要测量其内阻,可选用的器材如下:
A.待测电流表A1(量程0.6A)B.电压表V1(量程3V,内阻约2kΩ)
C.电压表V2(量程15V,内阻约10kΩ) D.滑动变阻器R1(最大电阻10Ω)
E.定值电阻R2(阻值5Ω) F.电源E(电动势4V)
G.电键S及导线若干
(1)电压表应选用_____________;
(2)画出实验电路图;
(3)如测得电压表的读数为V,电流表的读数为I,则电流表A1内阻的表达式为:RA= ______________。