(本小题满分14分)已知函数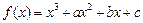 在
在 处的切
处的切 线方程为
线方程为 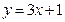 ,
,
(1)若函数 在
在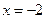 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)在(1)条件下,若函数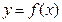 在
在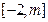 上的值域为
上的值域为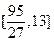 ,求m的取值范围;
,求m的取值范围;
(3)若函数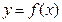 在区间
在区间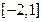 上
上 单调递增,求b的取值范围. [
单调递增,求b的取值范围. [
在平面直角坐标系 中,已知点
中,已知点
 ,点P是动点,且三角形
,点P是动点,且三角形 的三边所在直线
的三边所在直线
的斜率满足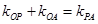 .
.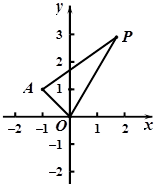
(1)求点P的轨迹 的方程;
的方程;
(2)设Q是轨迹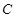 上异于点
上异于点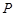 的一个点,若
的一个点,若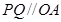 ,直线
,直线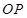 与
与 交于点M,探究是否存点P使得
交于点M,探究是否存点P使得 和
和 的面积满足
的面积满足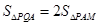 ,若存在,求出点P的坐标;若不存在,说明理由.
,若存在,求出点P的坐标;若不存在,说明理由.
设 为数列
为数列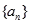 的前
的前 项和,对任意的
项和,对任意的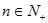 ,都有
,都有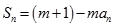
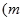 为常数,且
为常数,且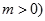 .
.
(1)求证:数列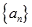 是等比数列;
是等比数列;
(2)设数列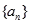 的公比
的公比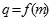 ,数列
,数列 满足
满足 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列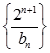 的前
的前 项和
项和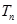 .
.
在四棱锥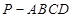 中,
中,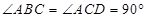 ,
,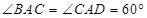 ,
, 平面
平面 ,
, 为
为 的中点,
的中点,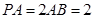 .
.
(1)求四棱锥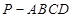 的体积
的体积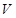 ;
;
(2)若 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面 ;
;
(3)求二面角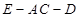 的大小.
的大小.
某校一课题小组对西安市工薪阶层对“楼市限购令”态度进行调查,抽调了50人,他们月收入频数分布及对“楼市限购令”赞成人数如下表.
| 月收入 (单位:百元) |
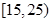 |
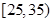 |
 |
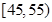 |
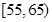 |
 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
3 |
1 |
(1)完成下图的月收入频率分布直方图(注意填写纵坐标);
(2)若从收入(单位:百元)在 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.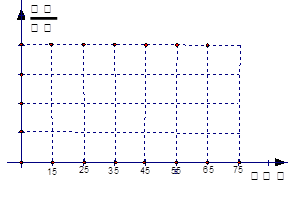
在 中,
中,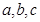 分别是角
分别是角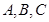 的对边,若
的对边,若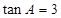 ,
,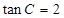 。
。
(1)求角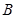 的大小; (2)若
的大小; (2)若 求
求 面积
面积