已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为 ,且过点M(4,
,且过点M(4,  )
)
(1)求双曲线方程;
(2)若点N(3、m)在双曲线上,求证:NF 1· NF2=0;
(3)求 F1NF2的面积
F1NF2的面积
(本题满分15分)已知椭圆 :
: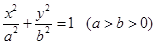 过点
过点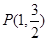 ,离心率为
,离心率为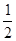 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设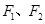 分别为椭圆
分别为椭圆 的左、右焦点,过
的左、右焦点,过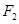 的直线
的直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,记
,记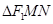 的内切圆的面积为
的内切圆的面积为 ,求当
,求当 取最大值时直线
取最大值时直线 的方程,并求出最大值.
的方程,并求出最大值.
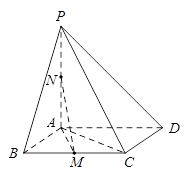
如图,在四棱锥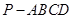 中,底面
中,底面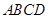 是平行四边形,
是平行四边形, 平面
平面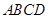 ,点
,点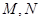 分别为
分别为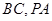 的中点,且
的中点,且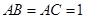 ,
, .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)设直线 与平面
与平面 所成角为
所成角为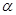 ,当
,当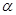 在
在 内变化时,求二面角
内变化时,求二面角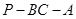 的取值范围.
的取值范围.
已知函数  .
.
(Ⅰ)求函数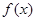 的单调增区间;
的单调增区间;
(Ⅱ)在 中,内角
中,内角 所对边分别为
所对边分别为 ,
,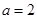 ,若对任意的
,若对任意的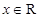 不等式
不等式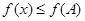 恒成立,求
恒成立,求 面积的最大值.
面积的最大值.
已知函数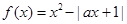 ,
,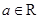 .
.
(1)若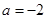 ,且存在互不相同的实数
,且存在互不相同的实数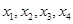 满足
满足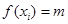
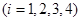 ,求实数
,求实数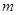 的取值范围;
的取值范围;
(2)若函数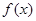 在
在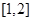 上单调递增,求实数
上单调递增,求实数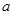 的取值范围.
的取值范围.
已知抛物线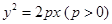 焦点为F,抛物线上横坐标为
焦点为F,抛物线上横坐标为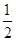 的点到抛物线顶点的距离与其到准线的距离相等.
的点到抛物线顶点的距离与其到准线的距离相等.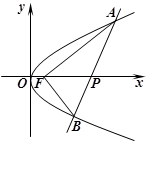
(1)求抛物线的方程;
(2)设过点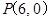 的直线
的直线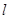 与抛物线交于
与抛物线交于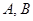 两点,若以
两点,若以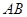 为直径的圆过点
为直径的圆过点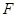 ,求直线
,求直线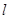 的方程.
的方程.