设函数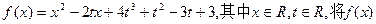 的最小值记为g(t).
的最小值记为g(t).
(1)求g(t)的表达式;
(2)讨论g(t)在区间[-1,1]内的单调性;
(3)当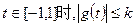 恒成立,其中k为正数,求k的取值范围.
恒成立,其中k为正数,求k的取值范围.
(本小题12分)某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.求该企业获得的最大利润.
(本小题12分)设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13
(Ⅰ)求{an}、{bn}的通项公式;
(Ⅱ)求数列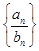 的前n项和Sn.
的前n项和Sn.
(本小题12分)等差数列 中,a3=2,a11=2a5
中,a3=2,a11=2a5
(I)求 的通项公式;
的通项公式;
(II)设
(本小题12分)已知等比数列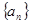 中,
中, ,求其第4项及前5项和.
,求其第4项及前5项和.
(本小题10分)若不等式 的解集是
的解集是 ,
,
(1)求 的值;
的值;
(2)求不等式 的解集.
的解集.