19.(本小题满分14分)设有关于 的一元二次
的一元二次
方程 .
.
(Ⅰ)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
2011年3月5日某校组织同学听取了温家宝总理所作的政府工作报告,并进行了检测,从参加检测的高一学生中随机抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)请根据频率分布直方图估计本次考试中的成绩的平均分及中位数(可保留一位小数).
下面是利用UNTIL循环设计的计算 的一个算法程序.
的一个算法程序.
S=1
I=1
DO
S=S*I
①
LOOP UNTIL ②
PRINT S
END
(Ⅰ)请将其补充完整;
(Ⅱ)绘制出该算法的流程图.
已知 ,
,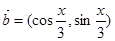 且
且
(1)求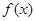 的周期;
的周期;
(2)求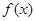 最大值和此时相应的
最大值和此时相应的 的值;
的值;
(3)求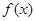 的单调增区间;
的单调增区间;
已知 ,
,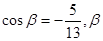 是第三象限角,求
是第三象限角,求 的值
的值
科已知 .
.
(1)若 ,求
,求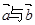 的夹角。
的夹角。
(2)若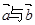 的夹角
的夹角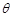 为45°,求
为45°,求 的值;
的值;