(本小题满分12分)
某市场搞国庆促销活动,一个人同时转动如图2所示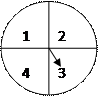
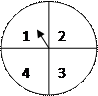 的两个转盘,记转盘(甲)得到的数
的两个转盘,记转盘(甲)得到的数 ,转盘(乙)
,转盘(乙)
得到的数为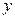 ,设
,设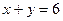 为中一等奖、
为中一等奖、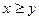
为中二等奖.
(Ⅰ)求中一等奖的概率; (甲) 图2 (乙)
(Ⅱ)求中二等奖的概率.
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列 的前4项,后6组的频数从左到右依次是等差数列
的前4项,后6组的频数从左到右依次是等差数列 的前6项.
的前6项.
(Ⅰ)求等比数列 的通项公式;
的通项公式;
(Ⅱ)求等差数列 的通项公式;
的通项公式;
(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率 的大小.
的大小.
已知等腰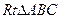 中,
中, .
.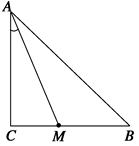
(Ⅰ)在线段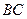 上任取一点
上任取一点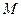 ,求使
,求使 的概率;
的概率;
(Ⅱ)在 内任作射线
内任作射线 ,求使
,求使 的概率.
的概率.
(本题满分18分,第1小题满分6分,第2小题满分6分,第3小题满分6分)
已知函数 ,如果存在给定的实数对(
,如果存在给定的实数对( ),使得
),使得 恒成立,则称
恒成立,则称 为“S-函数”.
为“S-函数”.
(1)判断函数 是否是“S-函数”;
是否是“S-函数”;
(2)若 是一个“S-函数”,求出所有满足条件的有序实数对
是一个“S-函数”,求出所有满足条件的有序实数对 ;
;
(3)若定义域为 的函数
的函数 是“S-函数”,且存在满足条件的有序实数对
是“S-函数”,且存在满足条件的有序实数对 和
和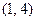 ,当
,当 时,
时, 的值域为
的值域为 ,求当
,求当 时函数
时函数 的值域.
的值域.
(本小题满分16分,第1小题满分4分,第2小题满分5分,第3小
题满分7分)
(1)若对于任意的 ,总有
,总有 成立,求常数
成立,求常数 的值;
的值;
(2)在数列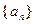 中,
中,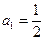 ,
,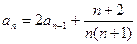 (
( ,
, ),求通项
),求通项 ;
;
(3)在(2)题的条件下,设 ,从数列
,从数列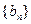 中依次取出第
中依次取出第 项,第
项,第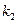 项,…第
项,…第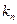 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列 ,其中
,其中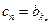 ,其中
,其中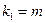 ,
, .试问是否存在正整数
.试问是否存在正整数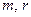 使
使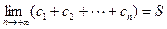 且
且 成立?若存
成立?若存 在,求正整数
在,求正整数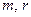 的值;不存在,说明理由.
的值;不存在,说明理由.
(本小题满分16分,第1小题满分6分,第2小题满分10分)
已知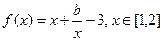
(1) 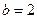 时,求
时,求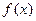 的值域;
的值域;
(2) 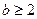 时,
时,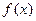 的最大值为M,最小值为m,且满足:
的最大值为M,最小值为m,且满足: ,求b的取值范围.
,求b的取值范围.