（本小题满分14分） 已知
（Ⅰ）求
；
（Ⅱ）若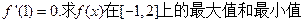
；
(Ⅲ)若
＜
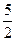，求证：当
和
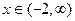时，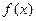
都是单调增函数．
设甲、乙两射手独立地射击同一目标，他们击中目标的概率分别为0．95，0．9．
求：
（1）在一次射击中，目标被击中的概率；
（2）目标恰好被甲击中的概率．
已知随机变量ε的分布列如下表：
| ε |
0 |
1 |
2 |
3 |
4 |
| p |
0．2 |
0．4 |
0．3 |
0．08 |
0．02 |
求其数学期望、方差和标准差．
某一中学生心理咨询中心服务电话接通率为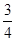
，某班3名同学商定明天分别就同一问题询问该服务中心，且每人只拨打一次，求他们中成功咨询的人数为X的分布列．
在一次口试中，要从10道题中随机抽出3道题进行回答，答对了其中2道题就获得及格，某考生会回答10道题中的6道题，那么他（她）获得及格的概率是多少？
一个袋子里有4个不同的红球，6个不同的白球，从中任取4个使得取出的球中红球比白球多的取法有多少种？红球不少于白球的取法又有多少种？