(本题16分)已知方程x2+y2－2x－4y+m=0．
（1）若此方程表示圆，求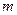
的取值范围；
（2）若(1)中的圆与直线x+2y－4=0相交于M，N两点，且OM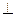
ON（O为坐标原点）求m的值；
（3）在(2)的条件下，求以MN为直径的圆的方程．
某导游团由外语导游10人，其中6人会说日语，现要选出4人去完成一项任务，求有两人会说日语的概率.
4名男生和2名女生中任选3人参加演讲比赛，设随机变量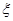
表示所选三人中女生人数.
（1）求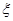得分布列；
（2）求所选三人中女生人数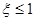
的概率.
某先生居住在城镇的A处,准备开车到单位B处上班，若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图所示.(例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为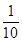
，路段CD发生堵车事件的概率为115).
(1)请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小；
(2)若记路线A→C→F→B中遇到堵车次数为随机变量X，求X的概率分布.
学校文娱队的每位队员唱歌、跳舞至少会一项，已知会唱歌的有2人，会跳舞的有5人，现从中选2人.设ξ为选出的人中既会唱歌又会跳舞的人数，且P(ξ＞0)＝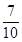
.
(1)求文娱队的人数；
(2)写出ξ的概率分布列.
在标准正态分布中我们常设P(X＜x0)＝Φ(x0)，根据标准正态曲线的对称性有性质：P(X＞x0)＝1-Φ(x0).若X～N(μ,σ2),记P(X＜x0)＝F(x0)＝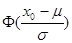
.
某中学高考数学成绩近似地服从正态分布N(100, 100)，求此校数学成绩在120分以上的考生占总人数的百分比.(Φ(2)≈0.977)