(本小题满分12分)已知圆C的圆心在直线y=2x上,且与直线l:x+y+1=0相切于点P(-1,0).
(Ⅰ)求圆C的方程;
(Ⅱ)若A(1,0),点B是圆C上的动点,求线段AB中点M的轨迹方程,并说明表示什么曲线.
已知函数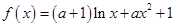 .
.
(1)讨论函数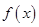 的单调性;
的单调性;
(2)设 ,证明:对任意
,证明:对任意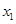 ,
,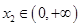 ,
, .
.
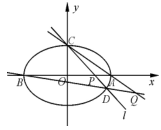
过点 的椭圆
的椭圆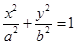 (
( )的离心率为
)的离心率为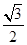 ,椭圆与
,椭圆与 轴交于两点
轴交于两点 、
、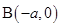 ,过点
,过点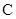 的直线
的直线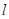 与椭圆交于另一点
与椭圆交于另一点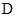 ,并与
,并与 轴交于点
轴交于点 ,直线
,直线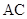 与直线
与直线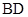 交于点
交于点 .
.
(1)当直线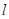 过椭圆右焦点时,求线段
过椭圆右焦点时,求线段 的长;
的长;
(2)当点 异于点
异于点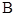 时,求证:
时,求证: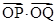 为定值.
为定值.
如图(1),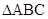 是等腰直角三角形,其中
是等腰直角三角形,其中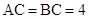 ,
,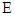 ,
,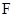 分别为
分别为 ,
,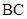 的中点,将
的中点,将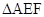 沿
沿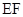 折起,点
折起,点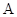 的位置变为点
的位置变为点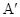 ,已知点
,已知点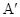 在平面上的射影
在平面上的射影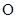 为
为 的中点,如图(2)所示.
的中点,如图(2)所示.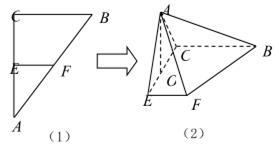
(Ⅰ)求证: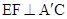 ;
;
(Ⅱ)求三棱锥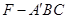 的体积.
的体积.
已知数列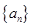 的前
的前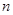 项和
项和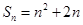 (
(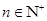 ),数列
),数列 的前
的前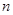 项和
项和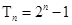 (
(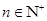 ).
).
(Ⅰ)求数列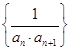 的前
的前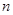 项和;
项和;
(Ⅱ)求数列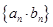 的前
的前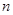 项和.
项和.
在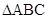 中,角
中,角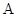 ,
,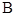 ,
,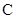 所对的边长分别为
所对的边长分别为 ,
,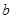 ,
,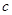 ,向量
,向量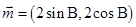 ,
,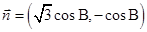 ,且
,且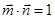 .
.
(1)求角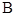 ;
;
(2)若 ,
,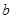 ,
,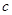 成等差数列,且
成等差数列,且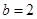 ,求
,求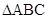 的面积.
的面积.