本题满分10分)2010年6月11日,第十九届世界杯在南非拉开帷幕.比赛前,某网站组织球迷对巴西、西班牙、意大利、英格兰四支夺冠热门球队进行竞猜,每位球迷可从四支球队中选出一支球队,现有三人参与竞猜
(1)若三人中每个人可以选择任一球队,且选择各个球队是等可能的,求四支球队中恰好有两支球队有人选择的概率;
(2)若三人中有一名女球迷,假设女球迷选择巴西队的概率为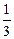 ,男球迷选择巴西队的概率为
,男球迷选择巴西队的概率为 ,记x为三人中选择巴西队的人数,求x的分布列和期望
,记x为三人中选择巴西队的人数,求x的分布列和期望
(本小题满分14分)
如图6,正方形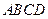 所在平面与三角形
所在平面与三角形 所在平面相交于
所在平面相交于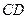 ,
, 平面
平面 ,且
,且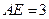 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求凸多面体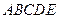 的体积.
的体积.
(本小题满分14分)
设数列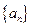 的前
的前 项和为
项和为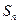 ,且对任意的
,且对任意的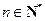 ,都有
,都有 ,
, .
.
(1)求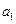 ,
,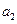 的值;(2)求数列
的值;(2)求数列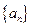 的通项公式
的通项公式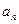 ;(3)证明:
;(3)证明: .
.
(本小题满分14分)
已知点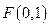 ,直线
,直线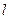 :
: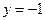 ,
,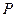 为平面上的动点,过点
为平面上的动点,过点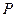 作直线
作直线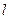 的垂线,垂足为
的垂线,垂足为 ,且
,且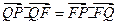 .(1)求动点
.(1)求动点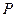 的轨迹
的轨迹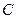 的方程;(2)已知圆
的方程;(2)已知圆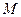 过定点
过定点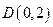 ,圆心
,圆心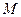 在轨迹
在轨迹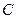 上运动,且圆
上运动,且圆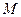 与
与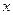 轴交于
轴交于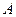 、
、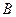 两点,设
两点,设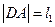 ,
,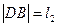 ,求
,求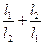 的最大值.
的最大值.
(本小题满分14分)已知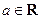 ,函数
,函数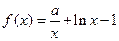 ,
,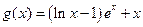 (其中
(其中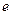 为自然对数的底数).(1)求函数
为自然对数的底数).(1)求函数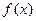 在区间
在区间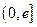 上的最小值;(2)是否存在实数
上的最小值;(2)是否存在实数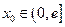 ,使曲线
,使曲线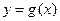 在点
在点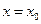 处的切线与
处的切线与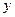 轴垂直? 若存在,求出
轴垂直? 若存在,求出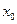 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)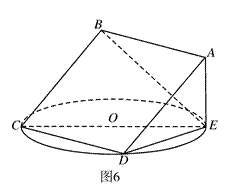
如图6,正方形 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于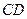 ,线段
,线段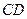 为圆
为圆 的弦,
的弦, 垂直于圆
垂直于圆 所在平面,垂足
所在平面,垂足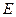 是圆
是圆 上异于
上异于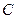 、
、 的点,
的点, ,圆
,圆 的直径为9.
的直径为9.
(1)求证:平面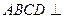 平面
平面 ;
;
(2)求二面角 的平面角的正切值.
的平面角的正切值.