(本小题满分14分)
已知点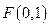 ,直线
,直线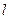 :
: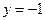 ,
,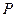 为平面上的动点,过点
为平面上的动点,过点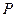 作直线
作直线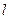 的垂线,垂足为
的垂线,垂足为 ,且
,且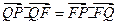 .(1)求动点
.(1)求动点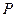 的轨迹
的轨迹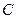 的方程;(2)已知圆
的方程;(2)已知圆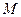 过定点
过定点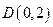 ,圆心
,圆心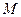 在轨迹
在轨迹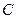 上运动,且圆
上运动,且圆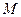 与
与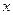 轴交于
轴交于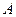 、
、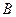 两点,设
两点,设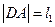 ,
,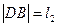 ,求
,求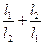 的最大值.
的最大值.
(本小题满分12分)
若(2x+4)2010=a0+a1x+a2x2+…+a2010x2010,则a0+a2+a4+…+a2010被3除的余数是多少?
又一年冬天即将来临,学校小卖部准备制订新一年的热饮销售计划. 根据去年的统计,当热饮单价为1.5元/杯时,每日可卖出热饮800杯,且热饮单价每提高1毛时,日销售量就降低20杯. 若该热饮成本为0.9元/杯,为使今年的热饮日销售利润不低于720元,应如何控制热饮的单价?
已知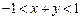 ,
,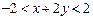 ,求
,求 的范围.
的范围.
求下列函数的最值.
(1)已知 ,求
,求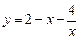 的最大值;
的最大值;
(2)已知 ,求
,求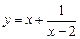 的最小值;
的最小值;
(3)已知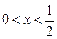 ,求
,求 的最大值.
的最大值.
数列{ }是公比为
}是公比为 的等比数列,
的等比数列,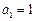 ,
,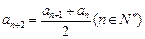
(1)求公比 ;
;
(2)令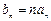 ,求{
,求{ }的前
}的前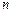 项和
项和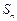 .
.