(本题满分10分) 如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它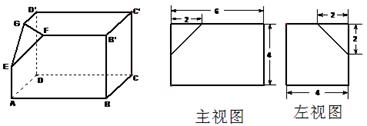
的主视图和左视图在右面画出(单位:cm).
(1)按照给出的尺寸,求该多面体的体积;
(2)在所给直观图中连结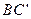 ,证明:
,证明: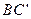 ∥面EFG。
∥面EFG。
(本小题满分7分)《选修4-4:坐标系与参数方程》
在直角坐标系xOy中,圆C的参数方程 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆C的交点为O,P,与直线
与圆C的交点为O,P,与直线 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
(本小题满分7分)选修4—2:矩阵与变换
若二阶矩阵 满足
满足 .
.
(Ⅰ)求二阶矩阵 ;
;
(Ⅱ)把矩阵 所对应的变换作用在曲线
所对应的变换作用在曲线 上,求所得曲线的方程.
上,求所得曲线的方程.
(本小题满分14分)已知函数 (其中
(其中 ,e是自然对数的底数,e=2.71828…).
,e是自然对数的底数,e=2.71828…).
(Ⅰ)当 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅲ)求证:对任意正整数n,都有 .
.
在平面直线坐标系XOY中,给定两点A(1,0),B(0,-2),点C满足 ,其中
,其中 ,且
,且 .
.
(1)求点C的轨迹方程.
(2)设点C的轨迹与双曲线 (
( )相交于M,N两点,且以MN为直径的圆经过原点,求证:
)相交于M,N两点,且以MN为直径的圆经过原点,求证: 是定值.
是定值.
(3)在(2)条件下,若双曲线的离心率不大于 ,求该双曲线实轴的取值范围.
,求该双曲线实轴的取值范围.
(本小题满分12分)在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
(Ⅰ)若从甲、乙两名学生中选择1人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(Ⅱ)若从学生甲的6次培训成绩中随机选择2个,记选到的分数超过87分的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.