(本小题满分14分)已知双曲线 的左、右顶点分别为
的左、右顶点分别为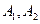 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.
(1)求直线 与
与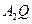 交点的轨迹E的方程
交点的轨迹E的方程
(2若过点 的两条直线
的两条直线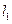 和
和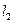 与轨迹E都只有一个交点,且
与轨迹E都只有一个交点,且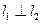 ,求
,求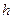 的值.
的值.
已知向量
(1)若 ,求
,求 的值;
的值;
(2)记 ,
, 在
在 中,角A、B、C的对边分别是
中,角A、B、C的对边分别是 ,且满
,且满 ,求
,求 的取值范围。
的取值范围。
已知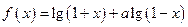 是奇函数。
是奇函数。
(1)求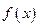 的定义域;(2)求
的定义域;(2)求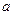 的值;
的值;
(3)当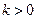 时,解关于
时,解关于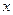 的不等式
的不等式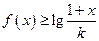 。
。
在一次数学考试中,第21题和第22题为选做题. 规定每位考生必须且只须在其中选做一题. 设4名考生选做每一道题的概率均为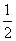 .
.
(1)求其中做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为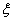 ,求
,求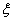 的概率分布及数学期望.
的概率分布及数学期望.
设函数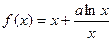 ,其中
,其中 为常数.
为常数.
(1)证明:对任意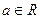 ,
,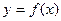 的图象恒过定点;
的图象恒过定点;
(2)当 时,判断函数
时,判断函数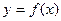 是否存在极值?若存在,证明你的结论并求出所有
是否存在极值?若存在,证明你的结论并求出所有
极值;若不存在,说明理由.
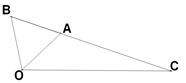
如图, 是等边三角形,
是等边三角形,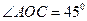 ,
,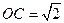 ,
,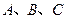 三点共线,
三点共线,
(1)求
(2)D是线段BC上的任意点,若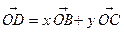 ,求
,求