（本小题满分12 分）
已知函数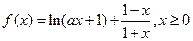
，其中
；
（1）若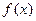
在x=1处取得极值，求
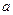的值；
（2）求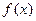的单调区间；
（3）若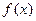的最小值为1，求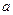的取值范围。
已知函数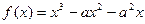
．
（1）若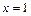
时函数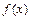
有极小值，求
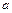的值；（2）求函数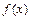的单调增区间．
已知函数
.
（1）求
的值；
（2）设
，求
的值.
已知函数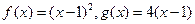
，数列
满足
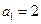，且
．
（1）试探究数列
是否是等比数列？
（2）试证明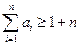
；
（3）设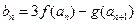
，试探究数列
是否存在最大项和最小项？若存在求出
最大项和最小项，若不存在，说明理由．
已知
是函数
的一个极值点。
（Ⅰ）求函数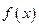
的单调区间；
（Ⅱ）若直线
与函数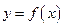
的图象有3个交点，求
的取值范围。
某公司生产陶瓷，根据历年的情况可知，生产陶瓷每天的固定成本为14000元，每生产一件产品，成本增加210元．已知该产品的日销售量
与产量
之间的关系式为
，每件产品的售价
与产量之间的关系式为
．
（Ⅰ）写出该陶瓷厂的日销售利润
与产量之间的关系式；
（Ⅱ）若要使得日销售利润最大，每天该生产多少件产品，并求出最大利润．