(本题满分10分)已知 向量
向量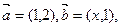
(1)当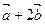 与
与 平行时,求
平行时,求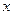 ;
;
(2)当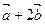 与
与 垂直时,求
垂直时,求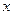 .
.
(本小题满分13分.其中(Ⅰ)小问6分,(Ⅱ)小问7分)
QQ先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).
(Ⅰ)求这7条鱼中至少有6条被QQ先生吃掉的概率;
(Ⅱ)以 表示这7条鱼中被QQ先生吃掉的鱼的条数,求
表示这7条鱼中被QQ先生吃掉的鱼的条数,求 的分布列及其数学期望
的分布列及其数学期望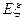 .
.
(本小题满分13分.其中(Ⅰ)小问6分,(Ⅱ)小问7分)
已知数列 满足:
满足:
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列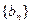 的前
的前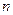 项和
项和
(本小题满分13分.其中(Ⅰ)小问6分,(Ⅱ)小问7分)
已知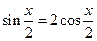 .
.
(Ⅰ)求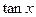 的值;
的值;
(Ⅱ)求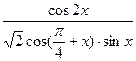 的值
的值
(本小题满分12分)
等比数列{ }的前n项和为
}的前n项和为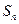 , 已知对任意的
, 已知对任意的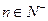 ,点
,点 均在函数
均在函数 (
(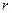 为常数)的图像上,数列
为常数)的图像上,数列 对任意的
对任意的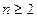 的正整数均满足
的正整数均满足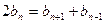 ,且
,且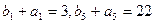
(I)求r的值和数列{ }的通项公式;
}的通项公式;
(II)求数列 的通项公式;
的通项公式;
(III)记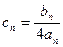 ,求数列
,求数列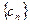 的前
的前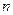 项和
项和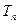 .
.
(本小题满分12分)
已知函数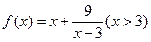
(I)求函数 的最小值;
的最小值;
(II)若不等式 恒成立,求实数
恒成立,求实数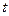 的取值范围。
的取值范围。