(本小题满分12分)
甲、乙等五名奥运志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加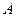 岗位服务的概率;
岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率。
(本小题满分12分)
已知 是定义在
是定义在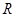 上的偶函数,当
上的偶函数,当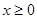 时,
时,
(1)求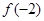
(2)求函数 的解析式;
的解析式;
(3)求 时,
时, 的值域
的值域
(本小题满分12分)
已知函数 的图象过点(0,-2),(2,0)
的图象过点(0,-2),(2,0)
(1)求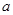 与
与 的值;
的值;
(2)求 时,
时, 的最大值与最小值.
的最大值与最小值.
(本小题满分10分)
如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,求此框架围成的面积y与x的函数式y="f" (x),并求出定义域。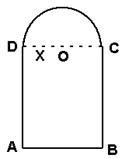
(本小题满分12分)
已知全集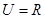 ,集合
,集合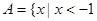 或
或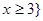 ,
,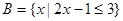 .
.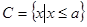
求:(1)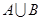
(2)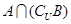
(3)若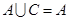 ,求实数
,求实数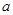 的范围.
的范围.
(本小题满分10分)
已知圆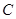 的圆心在
的圆心在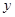 轴上,且圆
轴上,且圆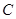 与直线
与直线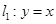 相切于点
相切于点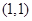 .
.
(1)求圆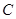 的方程;
的方程;
(2)若线段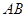 为圆
为圆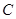 的直径,点
的直径,点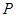 为直线
为直线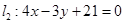 上的动点,求
上的动点,求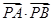 的最小值.
的最小值.