(本小题满分10分)
已知平面向量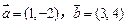 .
.
(1)求向量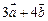 的坐标;
的坐标;
(2)当实数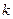 为何值时,
为何值时,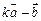 与
与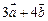 共线.
共线.
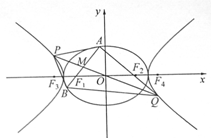
如图, 为坐标原点,椭圆 ( )的左右焦点分别为 ,离心率为 ;双曲线 的左右焦点分别为 ,离心率为 ,已知 ,且 .
(1)求 的方程;
(2)过 点作 的不垂直于 轴的弦 , 为 的中点,当直线 与 交于 两点时,求四边形 面积的最小值.
已知数列 满足 , , .
(1)若
为递增数列,且
成等差数列,求
的值;
(2)若
,且
是递增数列,
是递减数列,求数列
的通项公式.
如图,在平面四边形
中,
.
(1)求
的值;
(2)若
,
,求
的长.
某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为
和
,现安排甲组研发新产品
,乙组研发新产品
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品
研发成功,预计企业可获得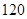 万元,若新产品
研发成功,预计企业可获得利润
万元,若新产品
研发成功,预计企业可获得利润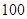 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
为圆周率,
为自然对数的底数.
(1)求函数
的单调区间;
(2)求
,
,
,
,
,
这6个数中的最大数与最小数;
(3)将
,
,
,
,
,
这6个数按从小到大的顺序排列,并证明你的结论.