(本小题满分14分)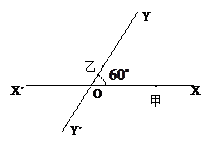
如图，有两条相交成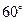
的直路
，
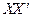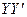，交点是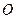
，甲、乙分别在
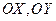上，起初甲离O点3 km，乙离O点1 km，后甲沿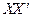方向用2 km/h的速度，乙沿
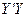方向用4km/h的速度同时步行. 设t小时后甲在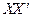上点A处，乙在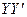上点B处.
（Ⅰ）求t=1.5时，甲、乙两人之间的距离；
（Ⅱ）求t=2时，甲、乙两人之间的距离；
（Ⅲ） 当t为何值时，甲、乙两人之间的距离最短？
已知函数f(x)＝
m(x－1)2－2x＋3＋ln x，m≥1.
(1)当m＝
时，求函数f(x)在区间[1,3]上的极小值；
(2)求证：函数f(x)存在单调递减区间[a，b]；
(3)是否存在实数m，使曲线C：y＝f(x)在点P(1,1)处的切线l与曲线C有且只有一个公共点？若存在，求出实数m的值；若不存在，请说明理由．
已知a∈R，函数f(x)＝4x3－2ax＋a.
(1)求f(x)的单调区间；
(2)证明：当0≤x≤1时，f(x)＋|2－a|＞0.
已知函数f(x)＝－x3＋ax2－4(a∈R)．
(1)若函数y＝f(x)的图象在点P(1，f(1))处的切线的倾斜角为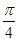
，求f(x)在[－1,1]上的最小值；
(2)若存在x0∈(0，＋∞)，使f(x0)＞0，求a的取值范围．
一火车锅炉每小时煤的消耗费用与火车行驶速度的立方成正比，已知当速度为20 km/h时，每小时消耗的煤价值40元，其他费用每小时需400元，火车的最高速度为100 km/h，火车以何速度行驶才能使从甲城开往乙城的总费用最少？
已知函数f(x)＝ln x＋ax(a∈R)．
(1)求f(x)的单调区间；
(2)设g(x)＝x2－4x＋2，若对任意x1∈(0，＋∞)，均存在x2∈[0,1]，使得f(x1)＜g(x2)，求a的取值范围．