已知数列 ,
, ,
, ,
,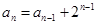 ,
, ,
, 为数列
为数列 的前
的前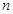 项和,
项和, 为数列
为数列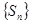 的前
的前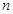 项和.
项和.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前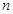 项和
项和 ;
;
(3)求证: .
.
在三棱锥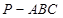 中,侧棱长均为
中,侧棱长均为 ,底边
,底边 ,
, ,
, ,
,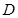 、
、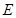 分别为
分别为 、
、 的中点.
的中点.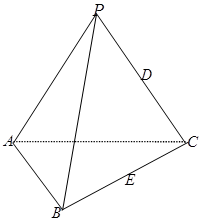
(1)求三棱锥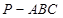 的体积;
的体积;
(2)求二面角 的平面角.
的平面角.
已知向量 ,
,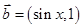 ,函数
,函数 .将函数
.将函数 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的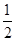 ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数
个单位,得到函数 的图象.
的图象.
(1)求函数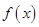 的单调递增区间;
的单调递增区间;
(2)若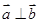 ,求
,求 的值.
的值.
如图,在三棱锥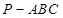 中,
中,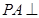 平面
平面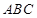 ,
,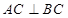 ,
,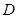 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.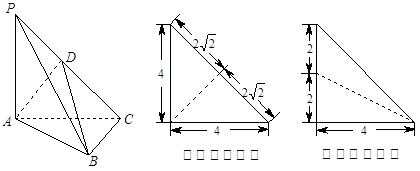
(1)证明: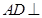 平面
平面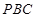 ;
;
(2)在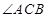 的平分线上确定一点
的平分线上确定一点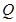 ,使得
,使得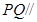 平面
平面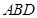 ,并求此时
,并求此时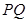 的长.
的长.
设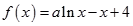 ,其中
,其中 ,曲线
,曲线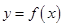 在点
在点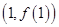 处的切线垂直于
处的切线垂直于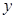 轴.
轴.
(1)求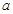 的值;
的值;
(2)求函数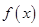 的极值.
的极值.