设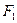 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)若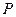 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求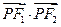 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点 的直线
的直线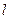 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、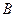 ,且∠
,且∠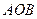 为钝角(其中
为钝角(其中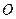 为坐标原点),求直线
为坐标原点),求直线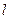 的斜率
的斜率 的取值范围.
的取值范围.
如图所示的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,BB1= ,M是线段B1D1的中点.
,M是线段B1D1的中点.
(1)求证:BM∥平面D1AC;
(2)求证:D1O⊥平面AB1C;
(3)求二面角B-AB1-C的大小.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.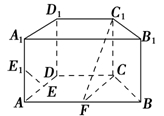
(1)证明:直线EE1∥平面FCC1;
(2)求二面角B-FC1-C的余弦值.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB. 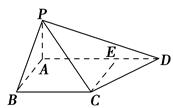
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=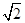 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.
已知Sn是数列{an}的前n项和,且an=Sn-1+2(n≥2),a1=2.
(1)求数列{an}的通项公式.
(2)设bn= ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
对于任意的正整数n,有Tn> 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.
已知等差数列{an}的前n项和为Sn,n∈N*,且a2=3,点(10,S10)在直线y=10x上.
(1)求数列{an}的通项公式;
(2)设bn=2an+2n,求数列{bn}的前n项和Tn.