已知抛物线 :
: 上一点
上一点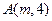 到其焦点的距离为
到其焦点的距离为 .
.
(I)求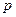 与
与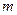 的值;
的值;
(II)设抛物线 上一点
上一点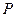 的横坐标为
的横坐标为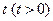 ,过
,过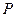 的直线交
的直线交 于另一点
于另一点 ,交
,交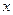 轴于点
轴于点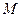 ,过点
,过点 作
作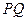 的垂线交
的垂线交 于另一点
于另一点 .若
.若 是
是 的切线,求
的切线,求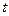 的最小值.
的最小值.
(本小题满分14分)
某公司经销某产品,第 天
天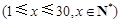 的销售价格为
的销售价格为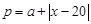 (
(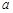 为常数)(元∕件),第
为常数)(元∕件),第 天的销售量为
天的销售量为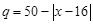 (件),且公司在第
(件),且公司在第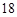 天该产品的销售收入为
天该产品的销售收入为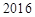 元.
元.
(1)求该公司在第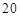 天该产品的销售收入是多少?
天该产品的销售收入是多少?
(2)这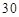 天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
(本小题满分14分)
如图,四棱锥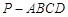 的底面
的底面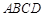 是边长为
是边长为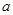 的正方形,
的正方形,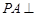 平面
平面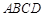 ,点
,点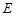 是
是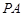 的中点.
的中点.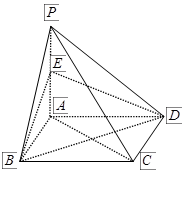
⑴求证: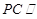 平面
平面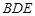 ;
;
⑵求证:平面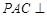 平面
平面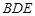 ;
;
⑶若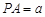 ,求三棱锥
,求三棱锥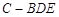 的体积.
的体积.
(本小题满分14分)
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)若 ,求函数
,求函数 的值域.
的值域.
(本小题满分15分)已知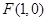 ,
, 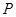 是平面上一动点,
是平面上一动点, 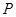 到直线
到直线 上的射影为点
上的射影为点 ,且满足
,且满足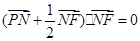
(1) 求点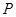 的轨迹
的轨迹 的方程;
的方程;
(2) 过点 作曲线
作曲线 的两条弦
的两条弦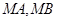 , 设
, 设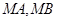 所在直线的斜率分别为
所在直线的斜率分别为 , 当
, 当 变化且满足
变化且满足 时,证明直线
时,证明直线 恒过定点,并求出该定点坐标。
恒过定点,并求出该定点坐标。
(本小题满分15分)已知函数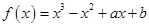 (
(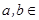 R)的一个极值点为
R)的一个极值点为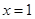 .
.
(1) 求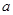 的值和
的值和 的单调区间;
的单调区间;
(2)若方程 的两个实根为
的两个实根为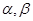
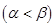 , 函数
, 函数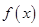 在区间
在区间 上单调,求
上单调,求 的取值范围。
的取值范围。