(本小题满分12分)
已知投资某项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是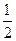 .设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为
.设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为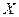 ,对该项目每投资十万元,
,对该项目每投资十万元,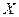 取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.
取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.
已知数列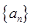 为等比数列,其前
为等比数列,其前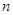 项和为
项和为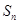 ,且满足
,且满足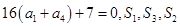 成等差数列.
成等差数列.
(1)求数列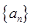 的通项公式;
的通项公式;
(2)已知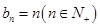 ,记
,记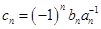 ,求数列
,求数列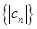 前
前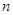 项和
项和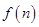 .
.
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
| 用煤(吨) |
用电(千瓦) |
产值(万元) |
|
| 甲产品 |
7 |
20 |
8 |
| 乙产品 |
3 |
50 |
12 |
但国家每天分配给该厂的煤、电有限,每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产量最大?最大日产量为多少?
已知 ;
; ,若
,若 是
是 的充分而不必要条件,求实数
的充分而不必要条件,求实数 的范围.
的范围.
已知A点坐标为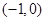 ,B点坐标为
,B点坐标为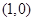 ,且动点
,且动点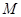 到
到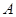 点的距离是
点的距离是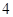 ,线段
,线段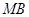 的
的
垂直平分线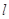 交线段
交线段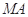 于点
于点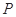 .
.
(1)求动点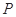 的轨迹C方程.
的轨迹C方程.
(2)若P是曲线C上的点,,求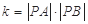 的最大值和最小值.
的最大值和最小值.
已知F1、F2是椭圆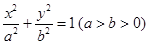 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足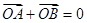 (O是坐标原点),
(O是坐标原点),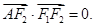 若椭圆的离心率等于
若椭圆的离心率等于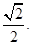
(1)求直线AB的方程;
(2)若三角形ABF2的面积等于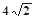 ,求椭圆的方程.
,求椭圆的方程.