(1)在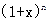 的展开式中,若第
的展开式中,若第 项与第
项与第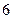 项系数相等,则
项系数相等,则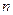 等于多少?
等于多少?
(2)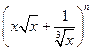 的展开式奇数项的二项式系数之和为
的展开式奇数项的二项式系数之和为 ,则求展开式中二项式系数最大的项
,则求展开式中二项式系数最大的项
(3)已知 展开式中的二项式系数的和比
展开式中的二项式系数的和比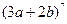 展开式的二项式系数的和大
展开式的二项式系数的和大 ,求
,求 展开式中的系数最大的项和系数最小的项
展开式中的系数最大的项和系数最小的项
已知圆C与两坐标轴都相切,圆心C到直线 的距离等于
的距离等于 .
.
(1)求圆C的方程.
(2)若直线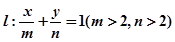 与圆C相切,求证:
与圆C相切,求证:
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击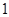 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击 次,求在这三枪中出现空弹的概率
次,求在这三枪中出现空弹的概率
已知椭圆 的焦点在
的焦点在 轴上,长轴长为
轴上,长轴长为 ,离心率为
,离心率为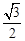 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点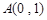 和直线
和直线 :
: ,线段
,线段 是椭圆
是椭圆 的一条弦且直线
的一条弦且直线 垂直平
垂直平
分弦 ,求实数
,求实数 的值.
的值.
已知 是函数
是函数 的一个极值点.
的一个极值点.


(1)求 的值;
的值;
(2)求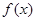 在区间
在区间 上的最值.
上的最值.
已知椭圆中心在原点,焦点在y轴上,焦距为4,离心率为 .
.
(1)求椭圆方程;
(2)设椭圆在y轴的正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段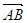 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.