甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击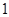 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击 次,求在这三枪中出现空弹的概率
次,求在这三枪中出现空弹的概率
已知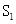 为直线
为直线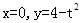 (
(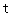 为常数)及
为常数)及 所围成的图形的面积,
所围成的图形的面积,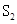 为直线
为直线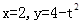 (
(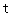 为常数)及
为常数)及 所围成的图形的面积,(如图)
所围成的图形的面积,(如图)
(1)当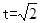 时,求
时,求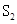 的值。
的值。
(2)若 ,求
,求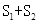 的最小值。
的最小值。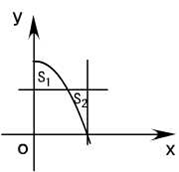
已知函数
(1)求函数 在区间
在区间 上的最大值和最小值,(
上的最大值和最小值,( 是自然对数的底数),
是自然对数的底数),
(2)求证:在区间 上,函数
上,函数 的图像在函数
的图像在函数 的图像的下方。
的图像的下方。
已知有如下等式: 当
当 时,试猜想
时,试猜想 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。
将4个编号为1,2,3,4的不同小球全部放入4个编号为1,2,3,4的4个不同盒子中,求:
(1)每盒至少一个球,有多少种放法?
(2)恰好有一个空盒,有多少种放法?
(3)每盒放一个球,并且恰好有一个球的编号与盒子的编号相同,有多少种放法?
(4)把已知中4个不同的小球换成四个完全相同的小球(无编号),其余条件不变,恰有一个空盒,有多少种放法?
已知复数 ,当实数m取何值时,复数
,当实数m取何值时,复数 是:
是:
(1)零;(2)纯虚数;(3)