锐角三角形ABC的内角A,B,C的对边分别为
(1)求B的大小;
(2)求 的取值范围.
的取值范围.
在△ABC中,已知 ,
, ,B=45°, 求A、C及c
,B=45°, 求A、C及c
如图,已知椭圆 到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点..
到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点..
(1)求此椭圆的方程及离心率;
(2)平行于AB的直线l与椭圆相交于P、Q两点,求|PQ|的最大值及此时直线l的方程.
已知,椭圆C以过点A(1, ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是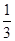 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(2)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.