锐角三角形ABC的内角A,B,C的对边分别为
(1)求B的大小;
(2)求 的取值范围.
的取值范围.
某商场销售某种商品的经验表明,该商品每日的销售量y(单
位:千克)与销售价格x(单位:元/千克)满足关系式y=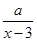 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
①求a的值;
②若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
在△ABC中,a、b、c分别为角A、B、C的对边,若m=(sin2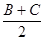 ,1),n="(-2,cos" 2A+1),且m⊥n.
,1),n="(-2,cos" 2A+1),且m⊥n.
(1)求角A的度数;
(2)当a=2 ,且△ABC的面积S=
,且△ABC的面积S= 时,求边c的值和△ABC的面积.
时,求边c的值和△ABC的面积.
△ABC为一个等腰三角形形状的空地,腰AC的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为S1和S2.
(1)若小路一端E为AC的中点,求此时小路的长度;
(2)若小路的端点E、F两点分别在两腰上,求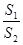 的最小值.
的最小值.
在△ABC中,a、b、c分别是角A、B、C所对的边,且a= c+bcosC.
c+bcosC.
(1)求角B的大小;
(2)若S△ABC= ,求b的最小值.
,求b的最小值.
在△ABC中,角A、B、C的对边分别为a、b、c,C=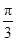 ,b=5,△ABC的面积为10
,b=5,△ABC的面积为10 .
.
(1)求a、c的值;
(2)求sin(A+ )的值.
)的值.