已知椭圆 的左、右焦点分别是
的左、右焦点分别是 ,
, ,如果椭圆
,如果椭圆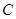 上的动点到点
上的动点到点 的距离的最大值是
的距离的最大值是 ,短轴一个端点到点
,短轴一个端点到点 的距离为
的距离为 .
.
(1)求椭圆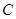 的方程;
的方程;
(2)设过点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆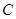 交于
交于 、
、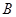 两点,求
两点,求 的面积.
的面积.
已知函数f (x) = 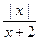
(1)判断函数f (x)在区间(0, +∞)上的单调性,并加以证明;
(2)如果关于x的方程f (x) = kx2有四个不同的实数解,求实数k的取值范围.
设函数 是R上的奇函数。
是R上的奇函数。
(Ⅰ)求a的值;(Ⅱ)求 的反函数;
的反函数;
(Ⅲ)若k ,解不等式:
,解不等式: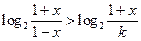
已知函数 有如下性质:如果常数
有如下性质:如果常数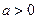 ,那么该函数在(0,
,那么该函数在(0, )上减函数,在
)上减函数,在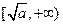 是增函数。
是增函数。
(1)如果函数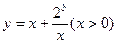 的值域为
的值域为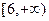 ,求
,求 的值;
的值;
(2)研究函数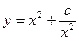 (常数
(常数 )在定义域的单调性,并说明理由;
)在定义域的单调性,并说明理由;
(3)对函数 和
和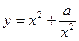 (常数
(常数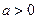 )作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
)作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数 (n是正整数)在区间[
(n是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论)。
,2]上的最大值和最小值(可利用你的研究结论)。
某市的出租车的价格规定:起步费11元,可行3千米;3千米后按每千米2.1元计价,可再行7千米;以后每千米都按3.15元计价,设每一次乘车的车费由行车里程确定.
(1)请写出一次乘车的车费y元与行车的里程x千米的函数关系;
(2)计算如果一次乘车费为32元,那么汽车行程为多少千米?
(3)请问当行程为28千米时,请你设计一种乘车方案,使总费用最省.
已知函数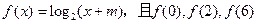 成等差数列.
成等差数列.
(Ⅰ)求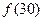 的值;
的值;
(Ⅱ)若a,b,c是两两不相等的正数,且a,b,c成等比数列,试判断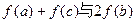 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.