已知函数 有如下性质:如果常数
有如下性质:如果常数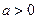 ,那么该函数在(0,
,那么该函数在(0, )上减函数,在
)上减函数,在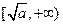 是增函数。
是增函数。
(1)如果函数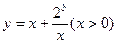 的值域为
的值域为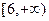 ,求
,求 的值;
的值;
(2)研究函数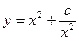 (常数
(常数 )在定义域的单调性,并说明理由;
)在定义域的单调性,并说明理由;
(3)对函数 和
和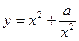 (常数
(常数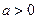 )作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
)作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数 (n是正整数)在区间[
(n是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论)。
,2]上的最大值和最小值(可利用你的研究结论)。
已知直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 是线段
是线段 上的一点,
上的一点, ,且点M在直线
,且点M在直线 上
上
(1)求椭圆的离心率;
(2)若椭圆的焦点关于直线 的对称点在单位圆
的对称点在单位圆 上,求椭圆的方程。
上,求椭圆的方程。
某商品每件成本9元,售价30元,每星期卖出432件。如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值 (单位:元,
(单位:元, )的平方成正比。已知商品单价降低2元时,一个星期多卖出24件。
)的平方成正比。已知商品单价降低2元时,一个星期多卖出24件。
(1)将一个星期的商品销售利润表示成 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
已知点 ,
, ,
, 在抛物线
在抛物线 (
(
 )上,
)上, 的重心与此抛物线的焦点F重合(如图)
的重心与此抛物线的焦点F重合(如图)
(1)写出该抛物线的方程和 焦点F的坐标;
焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程.
已知集合 在平面直角坐标系中,点M的坐标为(x,y) ,其中
在平面直角坐标系中,点M的坐标为(x,y) ,其中 。
。
(1)求点M不在x轴上的概率;
(2)求点M正好落在区域 上的概率。
上的概率。
(本小题满分12分)高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 |
频数 |
频率 |
 |
① |
② |
 |
0.050 |
|
 |
0.200 |
|
 |
12 |
0.300 |
 |
0.275 |
|
 |
4 |
③ |
 |
0.050 |
|
| 合 计 |
④ |
(1)根据上面图表,①、② 、③、④处的数值分别是多少?
、③、④处的数值分别是多少?
(2)在坐标系中画出 的频率分布直方图;
的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在 中的概率。
中的概率。