14分)某地计划从2006年起,用10年的时间创建50所“标准化学校”,已知该地在2006年投入经费为a万元,为保证计划的顺利落实,计划每年投入的经费都比上一年增加50万元。
(1)求该地第n年的经费投入y(万元)与n(年)的函数关系式;
(2)若该地此项计划的总投入为7250万元,则该地在2006年投入的经费a等于多少?
向量a=(cos23°,cos67°),向量b=(cos68°,cos22°).
(1)求a·b;
(2)若向量b与向量m共线,u=a+m,求u的模的最小值.
已知a=(cos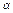 ,sin
,sin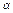 ),b=(cos
),b=(cos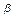 ,sin
,sin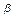 )(0<
)(0<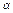 <
<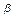 <
<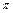 ).
).
(1)求证:a+b与a-b互相垂直;
(2)若ka+b与a-kb的模相等,求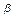 -
-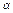 .(其中k为非零实数)
.(其中k为非零实数)
A(2,3),B(5,4),C(7,10), =
= +
+
 .当
.当 为何值时,
为何值时,
(1)点P在第一、三象限的角平分线上;
(2)点P到两坐标轴的距离相等?
在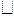 ABCD中,A(1,1),
ABCD中,A(1,1),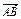 =(6,0),点M是线段AB的中点,线段CM与BD交于点P.
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.
(1)若 =(3,5),求点C的坐标;
=(3,5),求点C的坐标;
(2)当|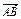 |=|
|=| |时,求点P的轨迹.
|时,求点P的轨迹.
若a,b为非零向量且a∥b,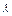 1,
1,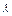 2∈R,且
2∈R,且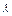 1
1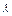 2≠0.
2≠0.
求证: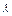 1a+
1a+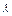 2b与
2b与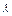 1a-
1a-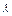 2b为共线向量.
2b为共线向量.