光线通过一块玻璃,其强度要损失10%,把几块这样的玻璃重叠起来,设光线原来的强度为k,通过x块玻璃以后强度为y.
(1)写出y关于x的函数关系式;
(2)通过多少块玻璃以后,光线强度将减弱到原来的 以下.(lg3≈0.477 1)
以下.(lg3≈0.477 1)
设在12个同类型的零件中有2个次品,抽取3次进行检验,每次任取一个,并且取出不再放回,若以 表示取出次品的个数. 求
表示取出次品的个数. 求 的分布列,期望及方差.
的分布列,期望及方差.
在一次数学考试中, 第14题和第15题为选做题.规定每位考生必须且只需在其中选做一题. 设4名考生选做这两题的可能性均为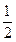 .
.
(1)其中甲、乙2名学生选做同一道题的概率;
(2)设这4名考生中选做第15题的学生数为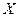 个,求
个,求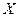 的分布列及数学期望.
的分布列及数学期望.
有A、B两个口袋,A袋中有6张卡片,其中1张写0,2张写1,3张写有2;B袋中7张卡片,其中4张写有0,1张写有1,2张写有2,从A袋中取1张卡片,B袋中取2张卡片,共3张卡片,
求:(1)取出的3张卡片都写0的概率;
(2)取出的3张卡片数字之积是4的概率;
(3)取出的3张卡片数字之积的数字期望。
在一次语文测试中,有一道我国四大文学名著《水浒传》、《三国演义》、《西游记》、《红楼梦》与它们的作者的连线题,已知连对一个得2分,连错一个不得分.
(Ⅰ)求该同学得分的分布列;
(Ⅱ)求该同学得分的数学期望.
某人在水池中养了10条金鱼,其中4条为白色,6条为红色,他每天随机地从水池中取出3条放入水箱中进行观察,观察后又把这3条放回水池中,连续5天的观察。
(1)问一天中,他取出两种颜色鱼的概率是多少?
(2)设随机变量X是取出两种颜色鱼的天数,求X的概率分布。