已知函数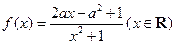 ,其中
,其中 .
.
(1)当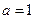 时,求曲线
时,求曲线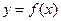 在点
在点 处的切线方程;
处的切线方程;
(2)当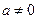 时,求函数
时,求函数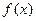 的单调区间与极值.
的单调区间与极值.
为了了解中学生的身高情况,对某校同龄的50名男学生的身体进行了测量,结果如下:(单位:cm)
175 168 170 176 167 181 162 173 171 177
171 171 174 173 174 175 177 166 163 160
166 166 163 169 174 165 175 165 170 158
174 172 166 172 167 172 175 161 173 167
170 172 165 157 172 173 166 177 169 181
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计中学生身高大于172 cm的学生所占的概率.
设甲袋装有m个白球,n个黑球,乙袋装有m个黑球,n个白球,从甲、乙袋中各摸一球.设事件A:“两球相同”,事件B:“两球异色”,试比较P(A) 与P(B)的大小.
某班有50名学生,在学校组织的一次数学质量抽测中,如果按照抽测成绩的分数段[60,65),[65,70),…,[95,100)进行分组,得到的分布情况如图3所示.求: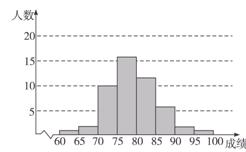
图3
(1)该班抽测成绩在[70,85)之间的人数;
(2)该班抽测成绩不低于85分的人数占全班总人数的百分比.
从个体数为103的总体中采用系统抽样,抽取一个容量为10的样本.写出具体的操作方法.
甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹。根据以往资料知,甲击中8环,9环,10环的概率分别为0.6,0.3,0.1,乙击中8环,9环,10环的概率分别为0.4,0.4,0.2。
设甲、乙的射击相互独立。
(Ⅰ)求在一轮比赛中甲击中的环数多于乙击中环数的概率;
(Ⅱ)求在独立的三轮比赛中,至少有两轮甲击中的环数多于乙击中环数的概率。