(本小题满分14分)
已知圆C过点P(1,1)且与圆M: 关于直线
关于直线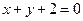 对称
对称
(1)求圆C的方程
(2)设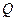 为圆C上一个动点,求
为圆C上一个动点,求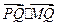 的最小值
的最小值
(3)过点P作两条相异直线分别与圆C相交于A、B两点,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP与AB是否平行,并请说明理由.
已知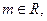 且复数z=(2+
且复数z=(2+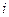 )
)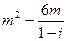

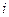 )在复平面内表示的点为A.
)在复平面内表示的点为A.
(1)当实数m取什么值时,复数z是纯虚数;
(2)当点A位于第二象限时,求实数m的取值范围.
已知一个四棱锥P—ABCD的三视图(正视图与侧视图为直角三角形,俯视图是带有一条对角形的正方形)如下,E是侧棱PC上的动点。
(1)求四棱锥P—ABCD的体积;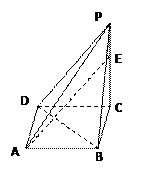 (2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
(2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
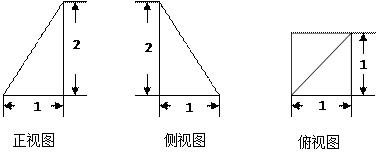 |
(本小题满分13分)
已知数列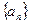 中,
中, 且点
且点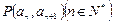 在直线
在直线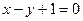 上。
上。
(1)求数列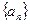 的通项公式;
的通项公式; (2)若函数
(2)若函数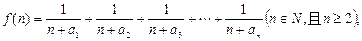 求函数
求函数 的最小值;
的最小值;
(3)设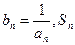 表示数列
表示数列 的前
的前 项和。试问:是否存在关于
项和。试问:是否存在关于 的整式
的整式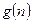 ,使得
,使得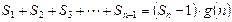 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出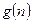 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
(本小题满分13分)
已知椭圆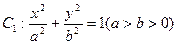 的离心率为
的离心率为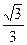 ,直线
,直线 与以原点为圆心、椭圆
与以原点为圆心、椭圆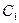 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。
(1)求椭圆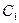 的方程;
的方程;
(2)设椭圆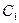 的左焦点为
的左焦点为 ,右焦点为
,右焦点为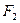 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直于直线
垂直于直线 ,垂足为点
,垂足为点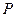 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹 的方程;
的方程;
(3)设 与
与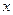 轴交于点
轴交于点 ,不同的两点
,不同的两点 在
在 上,且满足
上,且满足 ,求
,求 的取值范围。
的取值范围。
(本小题满分13分)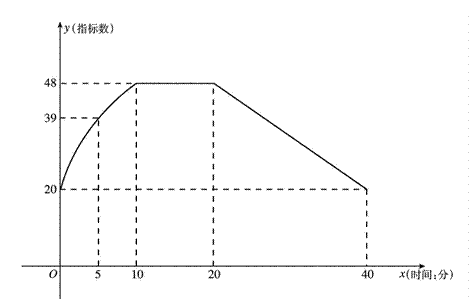
(本小题满分12分)通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散. 学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中). 当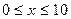 时,图象是抛物线的一部分,当
时,图象是抛物线的一部分,当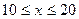 和
和 时,图象是线段.
时,图象是线段.
(1)当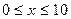 时,求注意力指标数y与时间x的函数关系式;
时,求注意力指标数y与时间x的函数关系式;
(2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.