(本小题满分12分)
某工厂师徒二人各加工相同型号的零件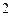 个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为
个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为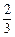 ,师徒二人各加工
,师徒二人各加工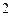 个零件都是精品的概率为
个零件都是精品的概率为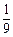 。
。
(1)求:徒弟加工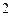 个零件都是精品的概率;
个零件都是精品的概率;
(2)求:徒弟加工该零件的精品数多于师父的概率;
(3)设师徒二人加工出的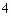 个零件中精品个数为
个零件中精品个数为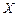 ,求:
,求: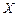 的分布列与均值
的分布列与均值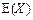 。
。
(本小题满分10分)
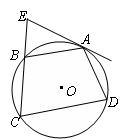
已知:如图,四边形ABCD内接于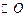 ,
,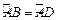 ,过
,过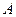 点的切线交
点的切线交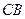 的延长线于
的延长线于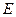 点.
点.
求证: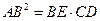 。
。
(本小题满分8分)
某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人。现从甲、乙两组中各抽取2名工人进行技术考核。
(1)求:抽出4人中恰有2名女工人的方法种数;
(2)求:从甲组抽取的工人中恰有1名女工人的概率;
(本小题满分12分)已知椭圆的两焦点为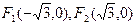 ,离心率
,离心率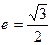 。
。
(1)求此椭圆的方程;
(2)设直线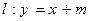 ,若
,若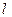 与此椭圆相交于P、Q两点,且
与此椭圆相交于P、Q两点,且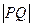 等于椭圆的短轴长,求m的值.
等于椭圆的短轴长,求m的值.
已知数列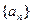 满足递推式
满足递推式 ,其中
,其中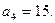
(Ⅰ)求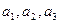 ;
;
(Ⅱ)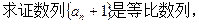 并求数列
并求数列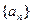 的通项公式;
的通项公式;
(Ⅲ)已知数列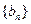 有
有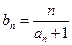 求数列
求数列 的前n项和
的前n项和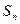 。
。