(本小题满分14分)
现在要对某个学校今年将要毕业的900名高三毕业生进行乙型肝炎病毒检验,可以利用两种方法.①对每个人的血样分别化验,这时共需要化验900次;②把每个人的血样分成两份,取其中m个人的血样各一份混合在一起作为一组进行化验,如果结果为阴性,那么对这m个人只需这一次检验就够了;如果结果为阳性,那么再对这m个人的另一份血样逐个化验,这时对这m个人一共需要m+1次检验.据统计报道,对所有人来说,化验结果为阳性的概率为0.1.
(1)求当m=3时,一个小组经过一次检验就能确定化验结果的概率是多少?
(2)试比较在第二种方法中,m=4和m=6哪种分组方法所需要的化验次数更少一些?
已知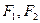 分别是椭圆
分别是椭圆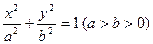 的左右焦点,其左准线与
的左右焦点,其左准线与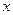 轴相交于点N,并且满足
轴相交于点N,并且满足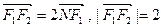 ,设A、B是上半椭圆上满足
,设A、B是上半椭圆上满足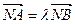 的两点,其中
的两点,其中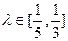 .(1)求此椭圆的方程;(2)求直线AB的斜率的取值范围.
.(1)求此椭圆的方程;(2)求直线AB的斜率的取值范围.
已知函数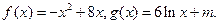 (1)求
(1)求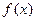 在区间
在区间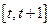 上的最大值
上的最大值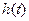 ;(2)若方程
;(2)若方程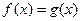 有且只有三个不同的实根,求实数
有且只有三个不同的实根,求实数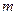 的取值范围.
的取值范围.
平面直角坐标系中,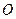 为坐标原点,给定两点
为坐标原点,给定两点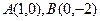 ,点
,点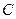 满足
满足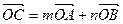 ,其中
,其中 ,且
,且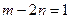 .(1)求点
.(1)求点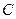 的轨迹方程;(2)设点
的轨迹方程;(2)设点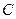 的轨迹与双曲线
的轨迹与双曲线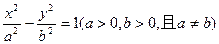 交于
交于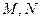 两点,且以
两点,且以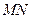 为直径的圆过原点,求证:
为直径的圆过原点,求证: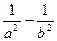 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于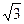 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
关于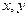 的方程
的方程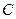 :
: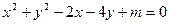 .(1)若方程
.(1)若方程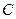 表示圆,求实数
表示圆,求实数 的范围;(2)在方程
的范围;(2)在方程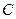 表示圆时,若该圆与直线
表示圆时,若该圆与直线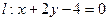 相交于
相交于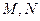 两点,且
两点,且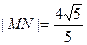 ,求实数
,求实数 的值;(3)在(2)的条件下,若定点
的值;(3)在(2)的条件下,若定点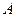 的坐标为(1,0),点
的坐标为(1,0),点 是线段
是线段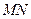 上的动点,求直线
上的动点,求直线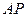 斜率的取值范围.
斜率的取值范围.
在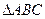 中,角
中,角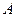 、
、 、
、 所对的边分别为
所对的边分别为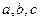 ,已知向量
,已知向量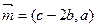
 ,且
,且 .(1)求角
.(1)求角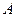 的大小;(2)若
的大小;(2)若 ,求
,求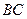 的最小值.
的最小值.