已知双曲线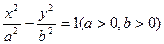 左右两焦点为
左右两焦点为 ,P为右支上一点,
,P为右支上一点, ,
,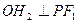 于H,
于H,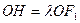 ,
,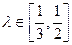 .
.
(1)求双曲线的离心率e的取值范围;
(2)当e取得最大值时,过 ,P的圆截y轴的线段长为4,求该圆方程.
,P的圆截y轴的线段长为4,求该圆方程.
在数列 中,
中, ,
, ,且
,且 (
(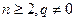 )。
)。
(Ⅰ)设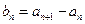 (
( ),求数列
),求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的通项公式。
的通项公式。
设函数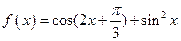 。
。
(Ⅰ)求函数 的最小正周期,并判断奇偶性;
的最小正周期,并判断奇偶性;
(Ⅱ)设A,B,C为 的三个内角,若
的三个内角,若 ,且C为锐角,求
,且C为锐角,求 。
。
已知函数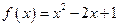 设计一个算法步骤求
设计一个算法步骤求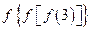 的值.
的值.
规定A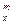 =x(x-1)…(x-m+1),其中x∈R,m为正整数,且A
=x(x-1)…(x-m+1),其中x∈R,m为正整数,且A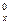 =1,这是排列数A
=1,这是排列数A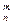 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.
(1)求A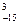 的值;
的值;
(2)排列数的两个性质:①A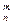 =nA
=nA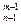 ,②A
,②A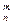 +mA
+mA =A
=A (其中m,n是正整数).是否都能推广到A
(其中m,n是正整数).是否都能推广到A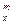 (x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(3)确定函数A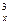 的单调区间.
的单调区间.
平面上有两个质点A(0,0), B(2,2),在某一时刻开始每隔1秒向上下左右任一方向移动一个单位。已知质点A向左,右移动的概率都是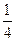 ,向上,下移动的概率分别是
,向上,下移动的概率分别是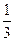 和P, 质点B向四个方向移动的概率均为q:
和P, 质点B向四个方向移动的概率均为q:
(1)求P和q的值;
(2)试判断至少需要几秒,A,B能同时到达D(1,2),并求出在最短时间同时到达的概率?