(本小题10分) 已知 ,
, ,当
,当 为何值时,
为何值时,
(Ⅰ)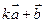 与
与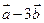 垂直?
垂直?
(Ⅱ) 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
(本小题满分14分)
如图所示,在所有棱长都为 的三棱柱
的三棱柱 中,侧棱
中,侧棱 ,
, 点为棱
点为棱 的中点.
的中点.
(1)求证: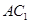 ∥平面
∥平面 ;
;
(2)求四棱锥 的体积.
的体积.
(本小题满分12分)某班 名学生在一次百米测试中,成绩全部介于
名学生在一次百米测试中,成绩全部介于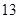 秒与
秒与 秒之间,将测试结果按如下方式分成五组:第一组
秒之间,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组 , ,第五组
, ,第五组 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.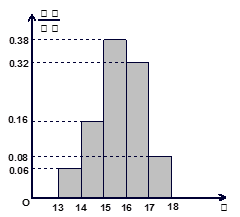
(1)根据频率分布直方图,估计这 名学生百米测试成绩的平均值;
名学生百米测试成绩的平均值;
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于 的概率.
的概率.
(本小题满分12分)已知函数
 的最小正周期为
的最小正周期为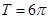 ,且
,且 .
.
(1)求 的表达式;
的表达式;
(2)设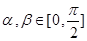 ,
, ,
, ,求
,求 的值.
的值.
(本小题满分14分)已知 ,函数
,函数 =
= .
.
(1)记 在区间
在区间 上的最大值为
上的最大值为 ,求
,求 的表达式;
的表达式;
(2)是否存在 ,使函数
,使函数 在区间
在区间 内的图象上存在两点,在该两点处的切线互相垂直?若存在,求
内的图象上存在两点,在该两点处的切线互相垂直?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分14分)在直角坐标系 中,曲线
中,曲线 上的点均在圆
上的点均在圆 外,且对
外,且对 上任意一点
上任意一点 ,
, 到直线
到直线 的距离等于该点与圆
的距离等于该点与圆 上点的距离的最小值.
上点的距离的最小值.
(1)求曲线 的方程;
的方程;
(2)设 为圆
为圆 外一点,过
外一点,过 作圆
作圆 的两条切线,分别与曲线
的两条切线,分别与曲线 相交于点
相交于点 和
和 .证明:当
.证明:当 在直线
在直线 上运动时,四点
上运动时,四点
 的纵坐标之积为定值.
的纵坐标之积为定值.