(本小题满分10分)
在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩再进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第三小组的频数是15.
(1) 求成绩在50-70分的频率是多少?
(2) 求这三个年级参赛学生的总人数是多少?
(3) 求成绩在80-100分的学生人数是多少?
(本小题共12分)“一站到底”是某电视台推出的大型游戏益智节目.某校高三年级为了解学生暑假期间的收视情况,从高中A,B层6个班共抽取了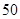 名学生,对他们累计收视时间进行统计,得到如下数据.
名学生,对他们累计收视时间进行统计,得到如下数据.
| 年级 |
人数 |
| A一班 |
4 |
| A二班 |
4 |
| A三班 |
6 |
| B四班 |
12 |
| B五班 |
6 |
| B六班 |
18 |
| 合计 |
50 |

请根据下面的各班人数统计表和收视时间的频率分布直方图解决下列问题:
(Ⅰ)抽查的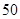 人中,累计收视时间为
人中,累计收视时间为 ~
~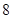 小时的人数有多少?
小时的人数有多少?
(Ⅱ)经调查,累计收视时间不少于 小时的学生均来自B层班.现采用分层抽样的方法,从累计收视时间不少于
小时的学生均来自B层班.现采用分层抽样的方法,从累计收视时间不少于 小时的学生中随机抽取
小时的学生中随机抽取 名学生进行问卷调查,求这三个班级各抽取了多少名学生;
名学生进行问卷调查,求这三个班级各抽取了多少名学生;
(Ⅲ)在(Ⅱ)抽取的 名学生中随机选取
名学生中随机选取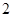 人进行访谈,求这
人进行访谈,求这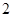 名学生来自不同班级的概率.
名学生来自不同班级的概率.
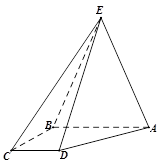
(本小题满分12分)如图,四棱锥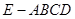 中,
中, ,
,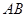 ∥
∥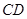 ,
, ,
, .
.
(1)求证: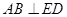 ;
;
(2)线段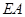 上若存在点
上若存在点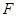 ,满足
,满足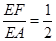 ,求证:
,求证: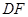 // 平面
// 平面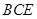 .
.
已知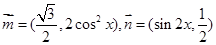 ,
,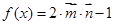 .
.
(I)求函数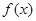 的单调递增区间;
的单调递增区间;
(II)函数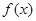 的图象可以由函数
的图象可以由函数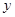
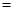
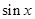 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
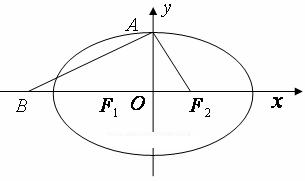
设椭圆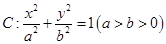 的左、右焦点分别为
的左、右焦点分别为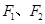 ,上顶点为
,上顶点为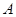 ,在
,在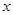 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且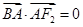 .
.
(1)求椭圆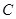 的离心率;
的离心率;
(2)若过 三点的圆与直线
三点的圆与直线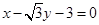 相切,求椭圆
相切,求椭圆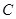 的方程;
的方程;
(3)在(2)的条件下,过右焦点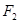 作斜率为
作斜率为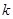 的直线
的直线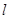 与椭圆
与椭圆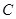 交于
交于 两点,线段
两点,线段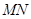 的中垂线与
的中垂线与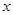 轴相交于
轴相交于 ,求实数
,求实数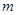 的取值范围.
的取值范围.
(本小题满分13分)已知函数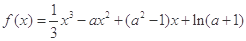 (其中
(其中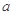 为常数).
为常数).
(1)若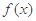 在区间
在区间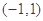 上不单调,求
上不单调,求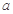 的取值范围;
的取值范围;
(2)记函数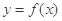 的极大值点为
的极大值点为 ,极小值点为
,极小值点为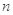 ,若
,若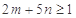 恒成立,试求
恒成立,试求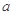 的取值范围;
的取值范围;
(3)若存在一条与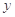 轴垂直的直线和函数
轴垂直的直线和函数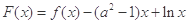 的图象相切,且切点的横坐标
的图象相切,且切点的横坐标 满足
满足 ,求实数
,求实数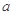 的取值范围.
的取值范围.