如图所示，两平行金属板A、B长l＝8cm，两板间距离d＝8cm，A板比B板电势高300V，即UAB＝300V．一带正电的粒子电量q＝10-10C，质量m＝10-20kg，从R点沿电场中心线垂直电场线飞入电场，初速度v0＝2×106m/s，粒子飞出平行板电场后经过界面MN、PS间的无电场区域后，进入固定在中心线上O点的点电荷Q形成的电场区域（设界面PS右边点电荷的电场分布不受界面的影响）．已知两界面MN、PS相距为L＝12cm，粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏EF上．（静电力常数k＝9×109N・m2/C2）求
（1）粒子穿过界面MN时的速度；
（2）粒子穿过界面PS时偏离中心线RO的距离多远；
（3）点电荷的电量．
一质量为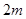
的物体P静止于光滑水平地面上，其截面如图所示。图中
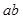为粗糙的水平面，长度为L；
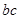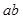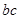为一光滑斜面，斜面和水平面通过与和均相切的长度可忽略的光滑圆弧连接。现有一质量为
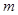的木块以大小为
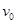的水平初速度从
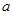点向左运动，在斜面上上升的最大高度为
，返回后在到达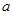点前与物体P相对静止。重力加速度为g。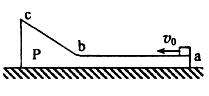
求（1）木块在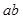段受到的摩擦力
；
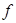（2）木块最后距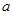点的距离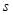
。
如图所示的水平转盘可绕竖直轴OO′旋转，盘上水平杆上穿着两个质量均为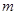
的小球A和B。现将A和B分别置于距轴
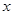和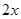
处，并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
。试分析转速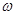
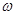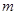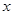从零逐渐增大，两球对轴保持相对静止过程中，在满足下列条件下，与、、的关系式。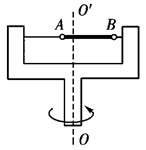
（1）绳中刚出现张力时；
（2）A球所受的摩擦力方向改变时；
（3）两球相对轴刚要滑动时。
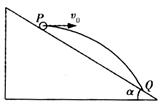
宇航员站在某质量分布均匀的星球表面一斜坡上P点，沿水平方向以初速度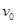
抛出一个小球，测得小球经时间
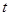落到斜坡另一点Q上，斜坡的倾角
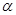，已知该星球的半径为
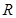，引力常量为
，求该星球的密度(已知球的体积公式是
)。
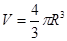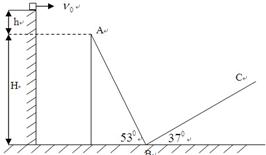
如图所示，一物块质量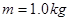
自平台上以速度
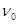水平抛出，刚好落在邻近一倾角为
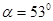的粗糙斜面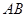
顶端，并恰好沿该斜面下滑，已知斜面顶端与平台的高度差
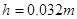，粗糙斜面
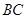倾角为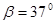
，足够长。物块与两斜面间的动摩擦因数均为
，
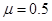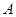点离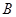
点所在平面的高度
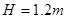。物块在斜面上运动的过程中始终未脱离斜面，不计在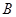点的机械能损失。最大静摩擦力等于滑动摩擦力，
,
。（
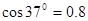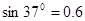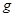取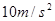
）
（1）物块水平抛出的初速度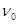是多少。
（2）若取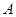所在水平面为零势能面，求物块第一次到达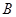点的机械能。
（3）从滑块第一次到达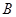点时起，经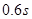
正好通过
点，求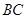之间的距离。
如图所示，M、N为纸面内两平行光滑导轨，间距为L。轻质金属杆a、b可在导轨上左右无摩擦滑动，杆与导轨接触良好，导轨右端与定值电阻连接。P、Q为平行板器件，两板间距为d，上下两板分别与定值电阻两端相接。两板正中左端边缘有一粒子源始终都有速度为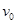
的带正电粒子沿平行于极板的方向进入两板之间。整个装置处于垂直于纸面向外的匀强磁场中。已知轻杆和定值电阻的阻值分别为r和R，其余电阻不计，带电粒子的重力不计，为使粒子沿原入射方向从板间右端射出，则轻杆应沿什么方向运动？速度多大？