如图,已知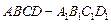 是
是 底面为正方形的长方体,
底面为正方形的长方体, ,
, ,点
,点 是
是 上的动点.
上的动点.
(1)试判断不论点 在
在 上的
上的 任何位置,是否都有平面
任何位置,是否都有平面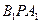 垂直于平面
垂直于平面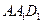 ?并证明你的结论;
?并证明你的结论;
(2)当 为
为 的中点时,求异面直线
的中点时,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)求 与平面
与平面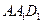
 所成角的正切值的最大值.
所成角的正切值的最大值.
已知函数f(x)的图象与函数h(x)=x+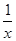 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+ ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
已知函数f(x)=xm-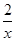 且f(4)=
且f(4)= .
.
(1)求m的值;
(2)判定f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
已知f(x)=x2+ax+3-a,若当x∈[-2,2]时,f(x)≥0恒成立,求a的取值范围.
已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.
(1)判断f(x)的奇偶性;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在区间[-3,3]上的值域;
(4)若∀x∈R,不等式f(ax2)-2f(x)<f(x)+4恒成立,求a的取值范围.
已知函数f(x)的定义域为{x|x∈R,且x≠0},对定义域内的任意x1、x2,都有f(x1·x2)=f(x1)+f(x2),且当x>1时,f(x)>0.
(1)求证:f(x)是偶函数;
(2)求证:f(x)在(0,+∞)上是增函数.