设函数 在
在 及
及 处有极值,
处有极值,
(1)求函数 的极值;
的极值;
(2)求函数 的增区间.
的增区间.
函数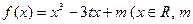 和
和 为实常数)是奇函数,设
为实常数)是奇函数,设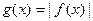 在
在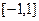 上的最大值为
上的最大值为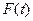 . ⑴求
. ⑴求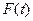 的表达式; ⑵求
的表达式; ⑵求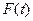 的最小值.
的最小值.
已知函数 的图象过原点,
的图象过原点,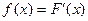 ,
, ,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
(1)若y=F(x)在x=-1处取得极大值2,求函数y=F(x)的单调区间;
(2)若使g(x)=0的x值满足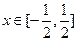 ,求线段AB在x轴上的射影长的取值范围;
,求线段AB在x轴上的射影长的取值范围;
已知函数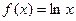
(1)求函数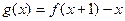 的最大值;
的最大值;
(2)当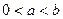 时,求证
时,求证 ;
;
函数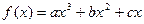 (
(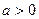 )的图象关于原点对称,
)的图象关于原点对称, 、
、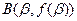 分别为函数
分别为函数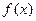 的极大值点和极小值点,且|AB|=2,
的极大值点和极小值点,且|AB|=2,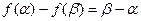 .
.
(Ⅰ)求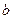 的值;
的值;
(Ⅱ)求函数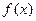 的解析式;
的解析式;
(Ⅲ)若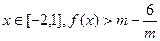 恒成立,求实数
恒成立,求实数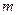 的取值范围.
的取值范围.
在平面直角坐标系中,O为坐标原点,已知点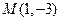 ,
,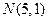 ,若点C满足
,若点C满足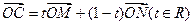 ,点C的轨迹与抛物线
,点C的轨迹与抛物线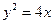 交于A、B两点.
交于A、B两点.
(I)求证: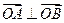 ;
;
(II)在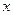 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点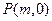 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.