(本小题满分13分)已知椭圆C: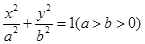 的离心率为
的离心率为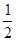 ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线 相切
相切
(Ⅰ)求椭圆C的标准方程
(Ⅱ)若直线L: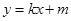 与椭圆C相交于A、B两点,且
与椭圆C相交于A、B两点,且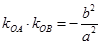 ,求证:
,求证: 的面积为定值
的面积为定值
假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5.记此时教室里敞开的窗户个数为X.
(1)求X的分布列;
(2)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为Y,求Y的数学期望.
已知⊙O′过定点A(0,p)(p>0),圆心O′在抛物线C:x2=2py(p>0)上运动,MN为圆O′在x轴上所截得的弦.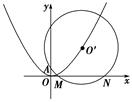
(1)当O′点运动时,|MN|是否有变化?并证明你的结论;
(2)当|OA|是|OM|与|ON|的等差中项时,试判断抛物线C的准线与圆O′的位置关系,并说明理由.
已知曲线E上任意一点P到两个定点F1(-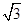 ,0)和F2(
,0)和F2(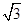 ,0)的距离之和为4.
,0)的距离之和为4.
(1)求曲线E的方程;
(2)设过点(0,-2)的直线l与曲线E交于C、D两点,且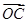 ·
·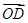 =0(O为坐标原点),求直线l的方程.
=0(O为坐标原点),求直线l的方程.
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为AD的中点.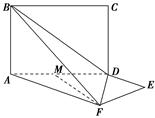
(1)证明:MF⊥BD;
(2)若二面角A-BF-D的平面角的余弦值为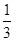 ,求AB的长.
,求AB的长.
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.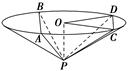
(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.