已知椭圆 :
: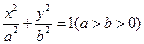 的离心率为
的离心率为 ,且过点
,且过点 ,设椭圆的右准线
,设椭圆的右准线 与
与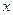 轴的交点为
轴的交点为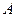 ,椭圆的上顶点为
,椭圆的上顶点为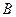 ,直线
,直线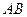 被以原点为圆心的圆
被以原点为圆心的圆 所截得的弦长为
所截得的弦长为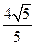 .
.
⑴求椭圆 的方程及圆
的方程及圆 的方程;
的方程;
⑵若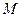 是准线
是准线 上纵坐标为
上纵坐标为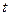 的点,求证:存在一个异于
的点,求证:存在一个异于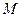 的点
的点 ,对于圆
,对于圆 上任意一点
上任意一点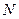 ,有
,有 为定值;且当
为定值;且当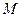 在直线
在直线 上运动时,点
上运动时,点 在一个定圆上.
在一个定圆上.
(本小题满分10分)
已知一条曲线上的点到定点 的距离是到定点
的距离是到定点 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程.
一袋中装有分别标记着1、2、3、4 数字的4个球, 从这只袋中每次取出1个球, 取出后放回, 连续取三次, 设三次取出的球中数字最大的数为ξ.(1) 求ξ=3时的概率; (2) 求ξ的概率分布列及数学期望.
甲、乙两人各射击一次,击中目标的概率分别是 .假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.
.假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.
在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(1)、试问此次参赛学生总数约为多少人?
(2)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可供查阅的(部分)标准正态分布表
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1.2 1.3 1.4 1.9 2.0 2.1 |
0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 |
0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 |
0.888 0.9066 0.9222 0.9726 0.9783 0.9830 |
0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 |
0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 |
0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 |
0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 |
0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 |
0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 |
0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
甲、乙、丙3人投篮,投进的概率分别是 ,
,  ,
,  .(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ
.(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ