已知 的图像与
的图像与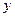 轴的交点为
轴的交点为 ,它在
,它在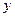 轴右侧的第一个最大值和最小值点分别为
轴右侧的第一个最大值和最小值点分别为 和
和
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间
的单调递增区间
(3)将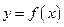 的图像上所有点的横坐标变为原来的
的图像上所有点的横坐标变为原来的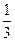 ,再将所得图像向右平移
,再将所得图像向右平移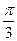 个单位得函数
个单位得函数 的图像,求
的图像,求 的解析式。
的解析式。
已知双曲线 的左顶点为
的左顶点为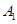 ,右焦点为
,右焦点为 ,
,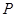 为双曲线右支上一点。
为双曲线右支上一点。
(1)求 的最小值;
的最小值;
(2)若直线 为圆
为圆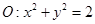 上动点
上动点 处的切线,且与双曲线
处的切线,且与双曲线 交于不同的两个点
交于不同的两个点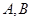 ,证明
,证明 为直角三角形。
为直角三角形。
已知函数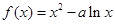 在
在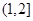 上是增函数,
上是增函数, 在
在 上为减函数.
上为减函数.
(1)求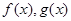 的表达式;
的表达式;
(2)当 时,若
时,若 在
在 内恒成立,求
内恒成立,求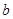 的取值范围.
的取值范围.
设 ,令
,令 ,又
,又 。
。
(1)求数列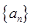 的通项公式;
的通项公式;
(2)求数列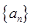 的前
的前 项和
项和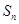 。
。
如图,四棱锥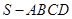 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的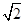 倍,
倍,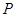 为侧棱
为侧棱 上的点。
上的点。
(Ⅰ)求证: ;
;
(Ⅱ)若 平面
平面 ,求二面角
,求二面角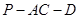 的大小;
的大小;
(Ⅲ)在(Ⅱ)的条件下,侧棱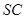 上是否存在一点
上是否存在一点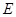 , 使得
, 使得 平面
平面 。若存在,求
。若存在,求 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。
某人投篮一次命中概率为 ,共投篮7次。
,共投篮7次。
(1)试问至多有1次命中的概率;
(2)试问出现命中次数为奇数的概率与命中次数为偶数的概率是否相等?请说明理由。