长度为L＝0.50m的轻质细杆OA，A端有一质量为m＝3.0-优题课

题文

长度为L＝0.50 m的轻质细杆OA，A端有一质量为m＝3.0 kg的小球，如图所示，小球以O点为圆心，在竖直平面内做圆周运动，通过最高点时，小球的速率是v＝2.0 m/s，g取10 m/s²，不计所有阻力，求：
（1）小球在最高点时对杆的作用力大小及方向？
（2）小球在最低点时对杆的作用力大小？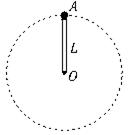

科目物理题型计算题难度较易

登录免费查看答案和解析

相关试题

半径为 $R$ ，均匀带正电荷的球体在空间产生球对称的电场；场强火小沿半径分布如图所示，图中 $E_{0}$ 已知， $E - r$ 曲线下 $O - R$ 部分的面积等于 $R - 2 R$ 部分的面积。

(1)写出 $E - r$ 曲线下面积的单位；
(2)己知带电球在 $r ⩾ R$ 处的场强 $E = k Q / r^{2}$ ，式中k为静电力常量，该均匀带电球所带的电荷量 $Q$ 为多大?
(3)求球心与球表面间的电势差 $△ R$ ；
(4)质量为 $m$ ，电荷量为 $q$ 的负电荷在球面处需具有多大的速度可以刚好运动到 $2 R$ 处?

如图，质量为 $M$ 、长为 $L$ 、高为h的矩形滑块置于水平地面上，滑块与地面间动摩擦因数为 $μ$ ；滑块上表面光滑，其右端放置一个质量为 $m$ 的小球。用水平外力击打滑块左端，使其在极短时间内获得向右的速度 $v_{0}$ ，经过一段时间后小球落地。求小球落地时距滑块左端的水平距离。

如图，柱形容器内用不漏气的轻质绝热活塞封闭一定量的理想气体，容器外包裹保温材料。开始时活塞至容器底部的高度为 $H_{1}$ ，容器内气体温度与外界温度相等。在活塞上逐步加上多个砝码后，活塞下降到距容器底部 $H_{2}$ 处，气体温度升高了 $△ T$ ；然后取走容器外的保温材料，活塞位置继续下降，最后静止于距容器底部 $H_{3}$ 处：已知大气压强为 $P_{0}$ 。求：气体最后的压强与温度。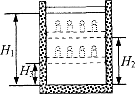

在科学研究中，可以通过施加适当的电场和磁场来实现对带电粒子运动的控制。如图所示的xOy平面处于匀强电场和匀强磁场中，电场强度 $E$ 和磁感应强度 $B$ 随时间 $t$ 做周期性变化的图象如图所示。x 轴正方向为 $E$ 的正方向，垂直纸面向里为 $B$ 的正方向。在坐标原点 $O$ 有一粒子 $P$ ，其质量和电荷量分别为 $m$ 和 $+ q$ .不计重力。在 $t = \frac{τ}{2}$ 时刻释放 $P$ ，它恰能沿一定轨道做往复运动。

（1）求 $P$ 在磁场中运动时速度的大小 $v_{0}$ ；
（2）求 $B_{0}$ 应满足的关系；
（3）在 $t_{0}$ （0＜ $t_{0}$ ＜ $\frac{τ}{2}$ ）时刻释放 $P$ ，求 $P$ 速度为零时的坐标。

如图所示，匀强磁场中有一矩形闭合线圈 $a b c d$ ，线圈平面与磁场垂直。已知线圈的匝数 $N = 100$ ，边长 $a b = 1.0 m$ 、 $b c = 0.5 m$ ，电阻 $r = 2 Ω$ 。磁感应强度 $B$ 在 $0 ~ 1 s$ 内从零均匀变化到 $0.2 T$ 。在 $1 ~ 5 s$ 内从 $0.2 T$ 均匀变化到 $- 0.2 T$ ，取垂直纸面向里为磁场的正方向。求：

（1） $0.5 s$ 时线圈内感应电动势的大小 $E$ 和感应电流的方向；

（2）在 $1 ~ 5 s$ 内通过线圈的电荷量 $q$ ；

（3）在 $0 ~ 5 s$ 内线圈产生的焦耳热 $Q$ 。

试卷网试题网古诗词网作文网范文网