(本小题满分10分)
已知平面向量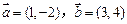 .
.
(1)求向量 的坐标;
的坐标;
(2)当实数 为何值时,
为何值时, 与
与 共线.
共线.
(本小题满分14分)
设函数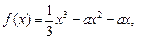
 .
.
(1) 试问函数f(x)能否在x=-1时取得极值?说明理由;
(2) 若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
(本小题满分12分)
已知{an}是递增的等差数列,满足a2·a4=3,a1+a5="4."
(1) 求数列{an}的通项公式和前n项和公式;
(2) 设数列{bn}对n∈N*均有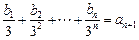 成立,求数列{bn}的通项
成立,求数列{bn}的通项 公式.
公式.
(本小题满分12分)
如图:在正方体ABCD—A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.
(1) 求证:面MNP∥面A1C1B;(2) 求证:MO⊥面A1C1.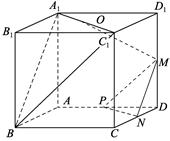
(本小题满分12分)
已知椭圆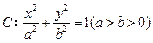 的离心率为
的离心率为 ,其中左焦点F(-2,0).
,其中左焦点F(-2,0).
(1) 求椭圆C 的方程;
的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
(本小题满分1 2分)
2分)
已知向量a=(2,1),b=(x,y).
(1) 若x∈{-1,0,1,2},y∈{-1,0,1},求向量a∥b的概率;
(2) 若x∈[-1,2],y∈[-1,1],求向量a,b的夹角是钝角的概率.