(本小题满分13分)
已知数列 满足:
满足: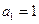 ,
,
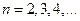
(I)求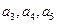 得值;
得值;
(II) 设 求证:数列
求证:数列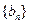 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(III) 对任意的 ,在数列
,在数列 中是否存在连续的
中是否存在连续的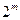 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这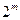 项,并证明这
项,并证明这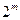 项构成等差数列;若不存在,说明理由。
项构成等差数列;若不存在,说明理由。
【2015高考浙江,文16】在 中,内角A,B,C所对的边分别为
中,内角A,B,C所对的边分别为 .已知
.已知 .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的面积.
的面积.
【2015高考新课标1,文17】(本小题满分12分)已知 分别是
分别是 内角
内角 的对边,
的对边, .
.
(Ⅰ)若 ,求
,求
(Ⅱ)若 ,且
,且 求
求 的面积.
的面积.
【2015高考天津,文16】(本小题满分13分)△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为 ,
,
(Ⅰ)求a和sinC的值;
(Ⅱ)求 的值.
的值.
【2015高考四川,文19】已知A、B、C为△ABC的内角,tanA、tanB是关于方程x2+ px-p+1=0(p∈R)两个实根.
px-p+1=0(p∈R)两个实根.
(Ⅰ)求C的大小
(Ⅱ)若AB=1,AC= ,求p的值
,求p的值
【2015高考陕西,文17】 的内角
的内角 所对的边分别为
所对的边分别为 ,向量
,向量 与
与 平行.
平行.
(Ⅰ)求 ;
;
(Ⅱ)若 求
求 的面积.
的面积.