【2015高考新课标1,文17】(本小题满分12分)已知 分别是
分别是 内角
内角 的对边,
的对边, .
.
(Ⅰ)若 ,求
,求
(Ⅱ)若 ,且
,且 求
求 的面积.
的面积.
已知椭圆 (
(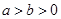 )的短轴长为2,离心率为
)的短轴长为2,离心率为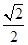 .过点M(2,0)的直线
.过点M(2,0)的直线 与椭圆
与椭圆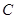 相交于
相交于 、
、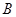 两点,
两点, 为坐标原点.
为坐标原点.
(1)求椭圆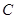 的方程;
的方程;
(2)求 的取值范围;
的取值范围;
(3)若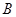 点关于
点关于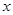 轴的对称点是
轴的对称点是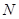 ,证明:直线
,证明:直线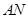 恒过一定点.
恒过一定点.
科学研究证实,二氧化碳等温室气体的排放(简称碳排放)对全球气候和生态环境产生了负面影响.环境部门对A市每年的碳排放总量规定不能超过550万吨,否则将采取紧急限排措施.已知A市2013年的碳排放总量为400万吨,通过技术改造和倡导低碳生活等措施,此后每年的碳排放量比上一年的碳排放总量减少10%.同时,因经济发展和人口增加等因素,每年又新增加碳排放量m万吨(m>0).
(1)求A市2015年的碳排放总量(用含m的式子表示);
(2)若A市永远不需要采取紧急限排措施,求m的取值范围.
如图,在三棱锥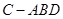 中,
中,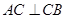 ,
,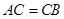 ,
,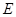 为
为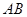 的中点,
的中点,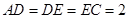 ,
,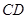 =
=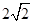 .
.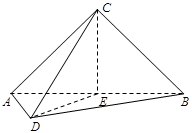
(1)求证:平面 ⊥平面
⊥平面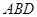 ;
;
(2)求直线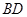 与平面
与平面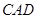 所成角的正弦值.
所成角的正弦值.
甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为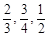 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.
(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量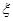 ,求随机变量
,求随机变量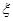 的分布列和数学期望
的分布列和数学期望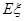 .
.
已知函数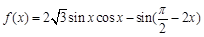 ,
,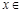 R.
R.
(1)求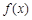 的最小值,并求出相应的
的最小值,并求出相应的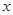 值的集合;
值的集合;
(2)求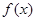 的单调递减区间.
的单调递减区间.