(满分12分)甲、乙两名同学在高一学年中(相同条件下)都参加数学考试十次,每次考试成绩如下表:
 次 次 数 数同学 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
| 甲 |
90 |
50 |
70 |
80 |
70 |
60 |
80 |
60 |
70 |
70 |
| 乙 |
20 |
40 |
60 |
80 |
70 |
70 |
80 |
90 |
90 |
100 |
请在坐标系中画出甲、乙两同学的成绩折线 图,并
图,并 从以下不同角度对这次测试结果进行分析。
从以下不同角度对这次测试结果进行分析。
(1)从平均数和方差相结合看,分析谁的成绩更稳定些;
(2)从平均数和中位数相结合看,分析谁的成绩好些;
(3)从平均数和成绩为90分以上的次数相结合看,分析谁的成绩好些 ;
(4)从折线图上两人成绩分数的走势看,分析谁更有潜力。
(本小题满分12分)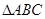 的内角
的内角 所对的边分别
所对的边分别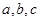 ,已知向量
,已知向量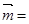
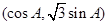 ,
,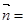
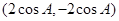 ,
, 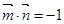 .
.
(1)若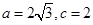 ,求
,求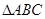 的面积;
的面积;
(2)求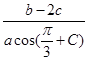 的值.
的值.
(本小题满分12分)正方形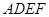 与梯形
与梯形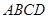 所在平面互相垂直,
所在平面互相垂直,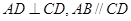 ,
,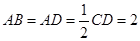 ,点M是EC中点.
,点M是EC中点.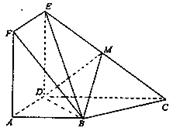
(1)求证:BM//平面ADEF;
(2)求三棱锥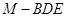 的体积.
的体积.
(本小题满分12分)已知函数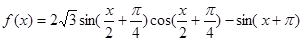 .
.
(1)求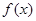 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(2)若将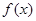 的图象向右平移
的图象向右平移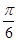 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间[0,π]上的最大值和最小值.
在区间[0,π]上的最大值和最小值.
(本小题满分12分)在等差数列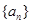 中,
中,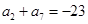 ,
,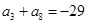 .
.
(1)求数列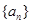 的通项公式;
的通项公式;
(2)设数列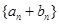 是首项为1,公比为
是首项为1,公比为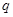 的等比数列,求
的等比数列,求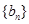 的前
的前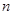 项和
项和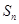 .
.
(本小题满分10分)选修4-5:不等式选讲
对于任意的实数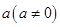 和
和 ,不等式
,不等式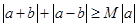 恒成立,记实数
恒成立,记实数 的最大值是
的最大值是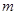 .
.
(1)求m的值;
(2)解不等式