(本小题满分12分)
已知向量 (
( 为常数且
为常数且 ),函数
),函数 在
在 上的最大值为
上的最大值为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)把函数 的图象向右平移
的图象向右平移 个单位,可得函数
个单位,可得函数 的图象,若
的图象,若 在
在 上为增函数,求
上为增函数,求 的最大值.
的最大值.
在等差数列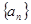 中,
中,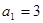 ,其前
,其前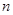 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数,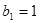 ,公比为
,公比为 ,且
,且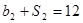 ,
, .
.
(1)求 与
与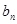 ;(2)设数列
;(2)设数列 满足
满足 ,求
,求 的前
的前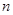 项和
项和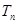 .
.
已知圆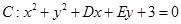 关于直线
关于直线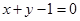 对称,圆心
对称,圆心 在第二象限,半径为
在第二象限,半径为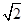 .
.
(1)求圆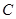 的方程;
的方程;
(2)是否存在直线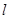 与圆
与圆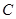 相切,且在
相切,且在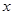 轴、
轴、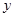 轴上的截距相等?若存在,求直线的方程;若不存在,说明理由.
轴上的截距相等?若存在,求直线的方程;若不存在,说明理由.
如图,在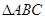 中,
中, ,点
,点 在
在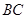 边上,且
边上,且
(1)求
(2)求 的长.
的长.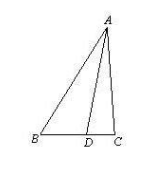
已知函数
(1)解不等式 ;
;
(2)若不等式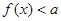 的解集为空集,求实数
的解集为空集,求实数 的取值范围.
的取值范围.
已知函数 的减区间是(-2,2)
的减区间是(-2,2)
(1)试求m,n的值;
(2)求过点 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;
(3)过点A(1,t),是否存在与曲线 相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.
相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.