(本小题满分10分)选修4—4 参数方程与极坐标
求圆 被直线
被直线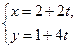 (
(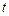 是参数
是参数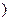 截得的弦长.
截得的弦长.
如图,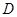 ,
,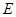 分别为
分别为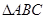 的边
的边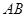 ,
, 上的点,且不与
上的点,且不与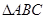 的顶点重合。已知
的顶点重合。已知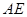 的长为
的长为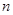 ,
, ,
,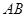 的长是关于
的长是关于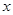 的方程x2-14x+mn=0的两个根。
的方程x2-14x+mn=0的两个根。
(Ⅰ)证明: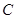 ,
,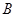 ,
,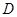 ,
,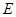 四点共圆;
四点共圆;
(Ⅱ)若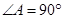 ,且
,且 ,求
,求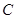 ,
,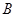 ,
,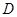 ,
,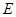 所在圆的半径。
所在圆的半径。
已知函数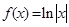
 ,函数
,函数
⑴当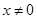 时,求函数
时,求函数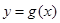 的表达式;
的表达式;
⑵若 ,函数
,函数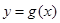 在
在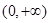 上的最小值是2 ,求
上的最小值是2 ,求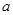 的值;
的值;
⑶在⑵的条件下,求直线
 与函数
与函数 的图象所围成图形的面积.
的图象所围成图形的面积.
设f(x)=2x3+ax+bx+1的导数为 ,若函数
,若函数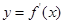 的图象关于直线
的图象关于直线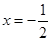 对称,且
对称,且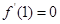 .](Ⅰ)求实数
.](Ⅰ)求实数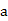 ,
, 的值;(5分)(Ⅱ)求函数
的值;(5分)(Ⅱ)求函数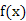 的极值
的极值
(1) 求圆心在直线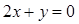 上,且与直线
上,且与直线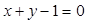 相切于点
相切于点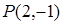 的圆的方程.
的圆的方程.
(2)求与圆 外切于(2,4)点且半径为
外切于(2,4)点且半径为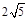 的圆的方程.
的圆的方程.
已知等比数列{an}的公比q=3,前3项和S3=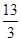 。(I)求数列{an}的通项公式;
。(I)求数列{an}的通项公式;
(II)若函数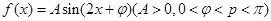 在
在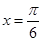 处取得最大值,且最大值为a3,求函数f(x)的解析式。
处取得最大值,且最大值为a3,求函数f(x)的解析式。